Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 137893 by bemath last updated on 07/Apr/21

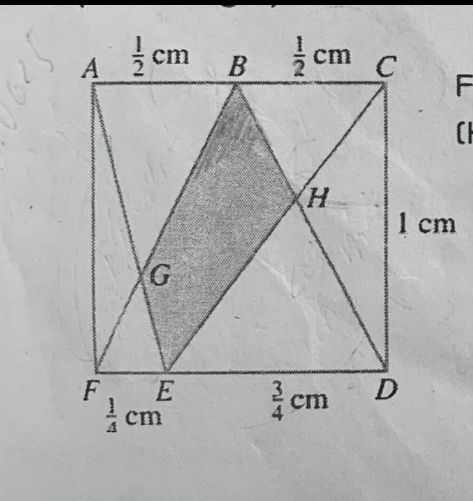
Answered by benjo_mathlover last updated on 08/Apr/21

$$byalgebra$$$$letF(0,0),D(1,0),A(0,1),C(1,1)$$$$B(\frac{1}{2},1),E(\frac{1}{4},0)$$$$eqoflineAE:x+\frac{1}{4}y=\frac{1}{4};$$$$eqoflineFB:y=2x$$$$intersectatpointG(\frac{1}{6},\frac{1}{3})$$$$eqoflineEC:4x-3y=1$$$$eqoflineBD:2x+y=2$$$$intersectatpointH(\frac{7}{10},\frac{3}{5})$$$$shadowofareais$$$$\frac{1}{2}\mid \left|\begin{array}{c}\frac{1}{4}0\\ \frac{7}{10}\frac{3}{5}\end{array}\right|+\left|\begin{array}{c}\frac{7}{10}\frac{3}{5}\\ \frac{1}{2}1\end{array}\right|+\left|\begin{array}{c}\frac{1}{2}1\\ \frac{1}{6}\frac{1}{3}\end{array}\right|+\left|\begin{array}{c}\frac{1}{6}\frac{1}{3}\\ \frac{1}{4}0\end{array}\right|\mid$$$$=\frac{1}{2}\mid (\frac{3}{20}+\frac{4}{10}+0-\frac{1}{12})\mid$$$$=\frac{1}{2}(\frac{11}{20}-\frac{1}{12})=\frac{7}{30}$$

Answered by mr W last updated on 08/Apr/21

$$\frac{EG}{GA}=\frac{\frac{1}{4}}{\frac{1}{2}}=\frac{1}{2}\Rightarrow EG=\frac{1}{2}GA=\frac{1}{3}AE$$$$\Rightarrow \mathrm{\Delta }EBG=\frac{1}{3}\mathrm{\Delta }EBA=\frac{1}{6}\mathrm{\Delta }EAC=\frac{[ACDF[}{12}$$$$\frac{EH}{HC}=\frac{\frac{3}{4}}{\frac{1}{2}}=\frac{3}{2}\Rightarrow EH=\frac{3}{2}HC=\frac{3}{5}EC$$$$\Rightarrow \mathrm{\Delta }EBH=\frac{3}{5}\mathrm{\Delta }EBC=\frac{3}{10}\mathrm{\Delta }EAC=\frac{3\left[ACDF\right]}{20}$$$$$$$$shadedarea=\mathrm{\Delta }EBG+\mathrm{\Delta }EBH$$$$=(\frac{1}{12}+\frac{3}{20})\left[ACDF\right]=\frac{7}{30}\times \left[ACDF\right]$$$$=\frac{7}{30}{cm}^2$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com