
Question Number 137864 by n0y0n last updated on 07/Apr/21
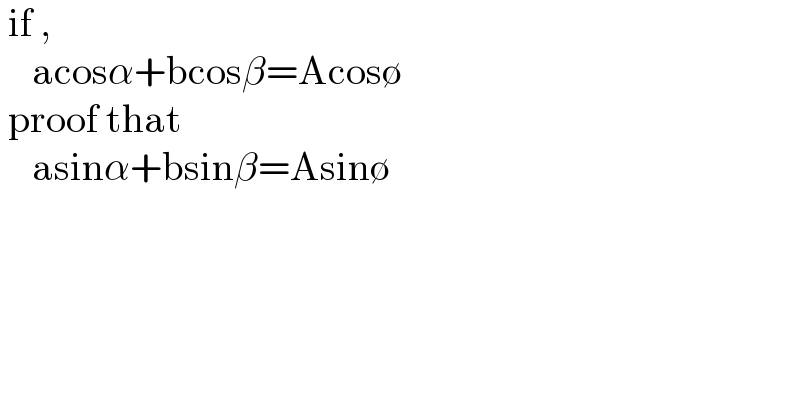
$$\:\mathrm{if}\:, \\ $$$$\:\:\:\:\mathrm{acos}\alpha+\mathrm{bcos}\beta=\mathrm{Acos}\emptyset \\ $$$$\:\mathrm{proof}\:\mathrm{that}\: \\ $$$$\:\:\:\:\mathrm{asin}\alpha+\mathrm{bsin}\beta=\mathrm{Asin}\emptyset \\ $$
Commented by mr W last updated on 07/Apr/21
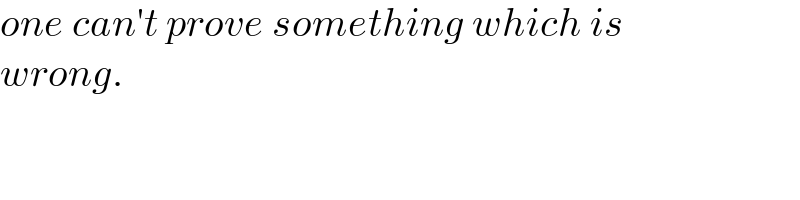
$${one}\:{can}'{t}\:{prove}\:{something}\:{which}\:{is} \\ $$$${wrong}. \\ $$
Commented by n0y0n last updated on 07/Apr/21

Commented by mr W last updated on 07/Apr/21
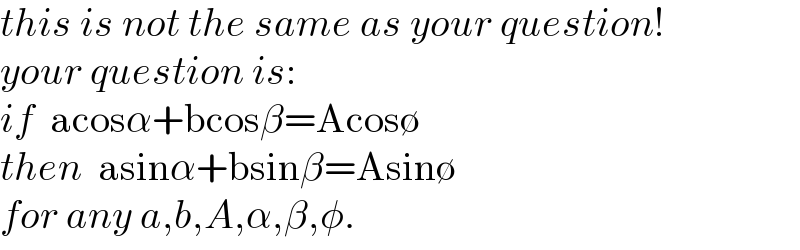
$${this}\:{is}\:{not}\:{the}\:{same}\:{as}\:{your}\:{question}! \\ $$$${your}\:{question}\:{is}: \\ $$$${if}\:\:\mathrm{acos}\alpha+\mathrm{bcos}\beta=\mathrm{Acos}\emptyset \\ $$$${then}\:\:\mathrm{asin}\alpha+\mathrm{bsin}\beta=\mathrm{Asin}\emptyset \\ $$$${for}\:{any}\:{a},{b},{A},\alpha,\beta,\phi. \\ $$
Commented by mr W last updated on 07/Apr/21

$${you}\:{should}\:{mean}\:{that}\:{constant} \\ $$$$\mathrm{acos}\alpha+\mathrm{bcos}\beta\:{can}\:{be}\:{expressed}\:{as}\:{A}\:\mathrm{cos}\:\phi \\ $$$${and}\:{constant} \\ $$$$\mathrm{asin}\:\alpha+\mathrm{bsin}\:\beta\:{can}\:{be}\:{expressed}\:{as}\:{A}\:\mathrm{sin}\:\phi. \\ $$$${this}\:{is}\:{true}. \\ $$$${generally}\:{any}\:{two}\:{constants},\:{say}\:{p}\: \\ $$$${and}\:{q},\:{can}\:{be}\:{expressed}\:{as} \\ $$$${p}={A}\:\mathrm{cos}\:\phi \\ $$$${q}={A}\:\mathrm{sin}\:\phi \\ $$$${with}\:{A}=\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} } \\ $$$$\phi=\mathrm{tan}^{−\mathrm{1}} \frac{{q}}{{p}} \\ $$
