
Question Number 137848 by Bekzod Jumayev last updated on 07/Apr/21
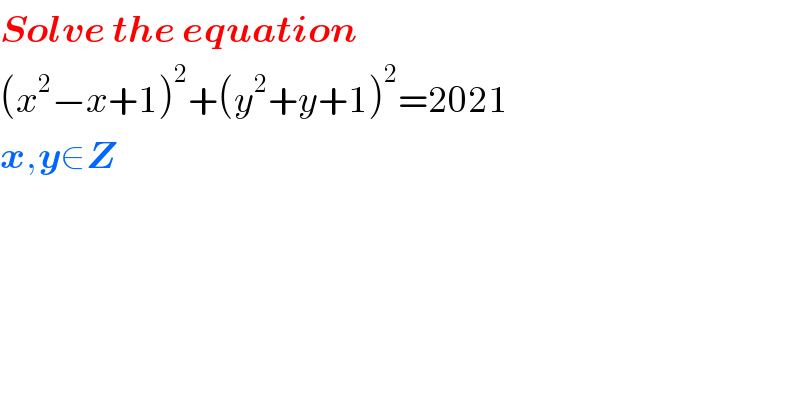
$$\boldsymbol{{Solve}}\:\boldsymbol{{the}}\:\boldsymbol{{equation}} \\ $$$$\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} +\left({y}^{\mathrm{2}} +{y}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{2021} \\ $$$$\boldsymbol{{x}},\boldsymbol{{y}}\in\boldsymbol{{Z}} \\ $$
Answered by mr W last updated on 07/Apr/21
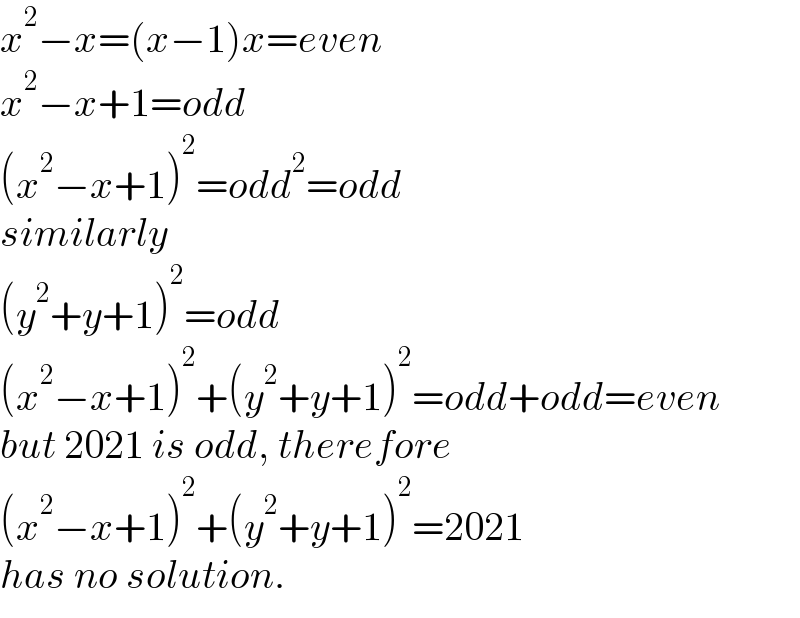
$${x}^{\mathrm{2}} −{x}=\left({x}−\mathrm{1}\right){x}={even} \\ $$$${x}^{\mathrm{2}} −{x}+\mathrm{1}={odd} \\ $$$$\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} ={odd}^{\mathrm{2}} ={odd} \\ $$$${similarly} \\ $$$$\left({y}^{\mathrm{2}} +{y}+\mathrm{1}\right)^{\mathrm{2}} ={odd} \\ $$$$\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} +\left({y}^{\mathrm{2}} +{y}+\mathrm{1}\right)^{\mathrm{2}} ={odd}+{odd}={even} \\ $$$${but}\:\mathrm{2021}\:{is}\:{odd},\:{therefore} \\ $$$$\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} +\left({y}^{\mathrm{2}} +{y}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{2021} \\ $$$${has}\:{no}\:{solution}. \\ $$
