Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 137817 by bramlexs22 last updated on 07/Apr/21

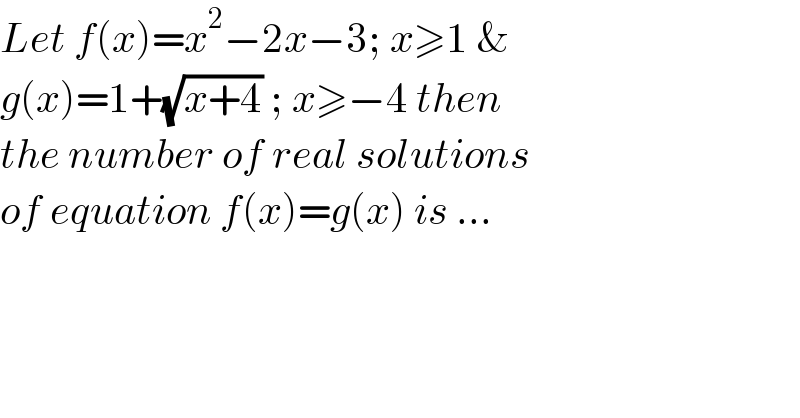
Let f(x)=x^2 −2x−3; x≥1 & g(x)=1+(√(x+4)) ; x≥−4 then the number of real solutions of equation f(x)=g(x) is ...

$${Let}\:{f}\left({x}\right)={x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{3};\:{x}\geqslant\mathrm{1}\:\& \\ $$ $${g}\left({x}\right)=\mathrm{1}+\sqrt{{x}+\mathrm{4}}\:;\:{x}\geqslant−\mathrm{4}\:{then} \\ $$ $${the}\:{number}\:{of}\:{real}\:{solutions} \\ $$ $${of}\:{equation}\:{f}\left({x}\right)={g}\left({x}\right)\:{is}\:... \\ $$

Answered by MJS_new last updated on 07/Apr/21

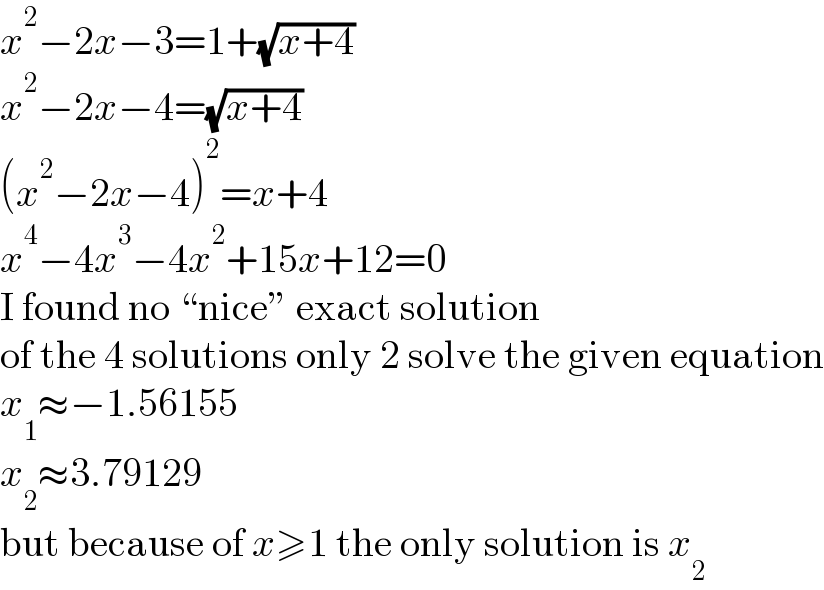
x^2 −2x−3=1+(√(x+4)) x^2 −2x−4=(√(x+4)) (x^2 −2x−4)^2 =x+4 x^4 −4x^3 −4x^2 +15x+12=0 I found no ♮niceε exact solution of the 4 solutions only 2 solve the given equation x_1 ≈−1.56155 x_2 ≈3.79129 but because of x≥1 the only solution is x_2

$${x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{3}=\mathrm{1}+\sqrt{{x}+\mathrm{4}} \\ $$ $${x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{4}=\sqrt{{x}+\mathrm{4}} \\ $$ $$\left({x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{4}\right)^{\mathrm{2}} ={x}+\mathrm{4} \\ $$ $${x}^{\mathrm{4}} −\mathrm{4}{x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} +\mathrm{15}{x}+\mathrm{12}=\mathrm{0} \\ $$ $$\mathrm{I}\:\mathrm{found}\:\mathrm{no}\:\natural\mathrm{nice}\varepsilon\:\mathrm{exact}\:\mathrm{solution} \\ $$ $$\mathrm{of}\:\mathrm{the}\:\mathrm{4}\:\mathrm{solutions}\:\mathrm{only}\:\mathrm{2}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{given}\:\mathrm{equation} \\ $$ $${x}_{\mathrm{1}} \approx−\mathrm{1}.\mathrm{56155} \\ $$ $${x}_{\mathrm{2}} \approx\mathrm{3}.\mathrm{79129} \\ $$ $$\mathrm{but}\:\mathrm{because}\:\mathrm{of}\:{x}\geqslant\mathrm{1}\:\mathrm{the}\:\mathrm{only}\:\mathrm{solution}\:\mathrm{is}\:{x}_{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com