
Question Number 137613 by physicstutes last updated on 04/Apr/21

$$\mathrm{Two}\:\mathrm{particles}\:\mathrm{of}\:\mathrm{mass}\:{m}\:\mathrm{and}\:\mathrm{4}{m}\:\mathrm{are}\:\mathrm{connected}\:\mathrm{by}\:\mathrm{a}\:\mathrm{light}\:\mathrm{inelastic} \\ $$$$\mathrm{string}\:\mathrm{of}\:\mathrm{length}\:\mathrm{3}{a},\:\mathrm{which}\:\mathrm{passes}\:\mathrm{through}\:\mathrm{a}\:\mathrm{small}\:\mathrm{smooth}\:\mathrm{fixed}\:\mathrm{ring}. \\ $$$$\mathrm{The}\:\mathrm{heavier}\:\mathrm{particle}\:\mathrm{hangs}\:\mathrm{at}\:\mathrm{rest}\:\mathrm{at}\:\mathrm{a}\:\mathrm{distance}\:\mathrm{2}{a}\:\mathrm{beneath}\:\mathrm{the}\:\mathrm{ring}, \\ $$$$\mathrm{while}\:\mathrm{the}\:\mathrm{lighter}\:\mathrm{particle}\:\mathrm{describes}\:\mathrm{a}\:\mathrm{horizontal}\:\mathrm{circle}\:\mathrm{with}\:\mathrm{constant} \\ $$$$\mathrm{speed}. \\ $$$$\:\mathrm{Find} \\ $$$$\left(\mathrm{a}\right)\:\mathrm{The}\:\mathrm{distance}\:\mathrm{of}\:\mathrm{the}\:\mathrm{plane}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circle}\:\mathrm{below}\:\mathrm{the}\:\mathrm{ring}. \\ $$$$\left(\mathrm{b}\right)\:\mathrm{The}\:\mathrm{angular}\:\mathrm{speed}\:\mathrm{of}\:\mathrm{the}\:\mathrm{lighter}\:\mathrm{particle}. \\ $$
Answered by mr W last updated on 04/Apr/21
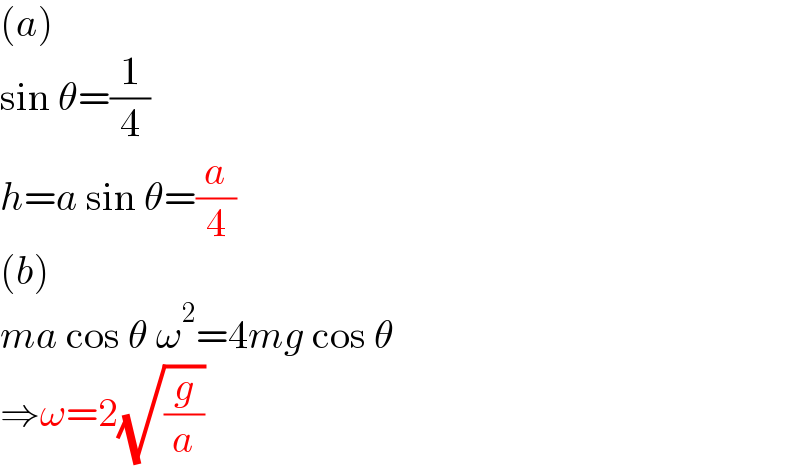
$$\left({a}\right) \\ $$$$\mathrm{sin}\:\theta=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${h}={a}\:\mathrm{sin}\:\theta=\frac{{a}}{\mathrm{4}} \\ $$$$\left({b}\right) \\ $$$${ma}\:\mathrm{cos}\:\theta\:\omega^{\mathrm{2}} =\mathrm{4}{mg}\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow\omega=\mathrm{2}\sqrt{\frac{{g}}{{a}}} \\ $$
Commented by physicstutes last updated on 04/Apr/21
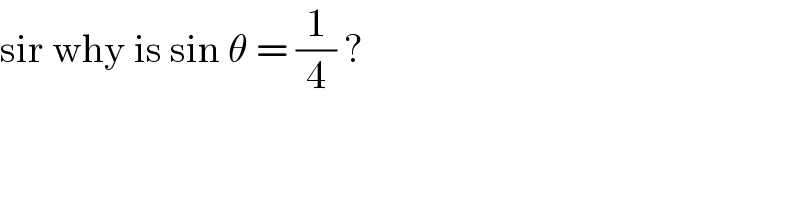
$$\mathrm{sir}\:\mathrm{why}\:\mathrm{is}\:\mathrm{sin}\:\theta\:=\:\frac{\mathrm{1}}{\mathrm{4}}\:? \\ $$
Commented by mr W last updated on 04/Apr/21
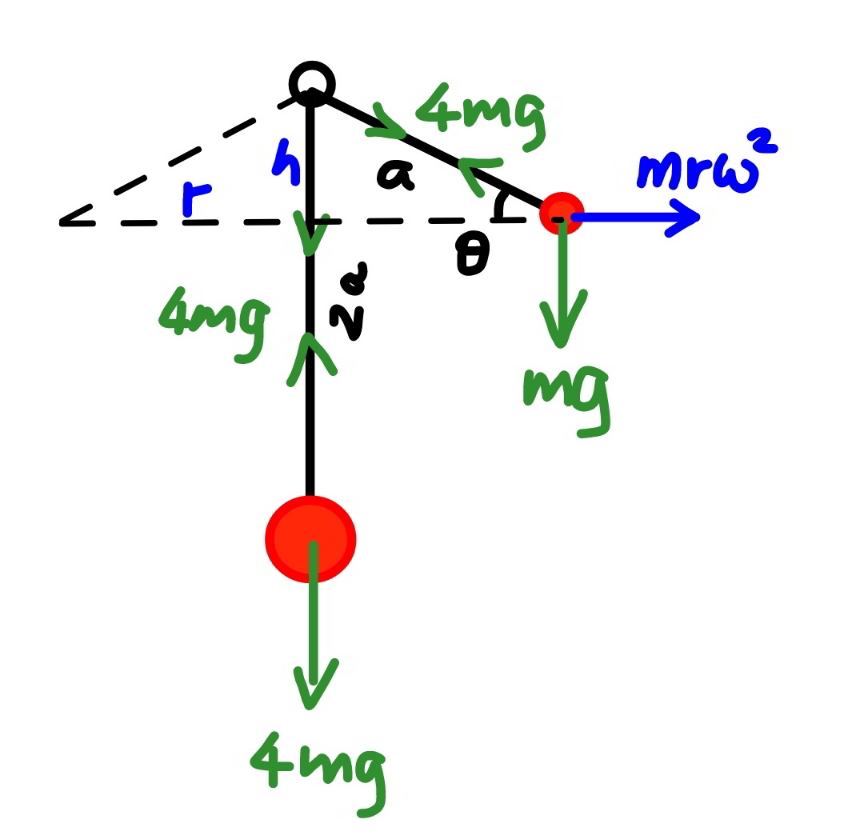
Commented by physicstutes last updated on 06/Apr/21
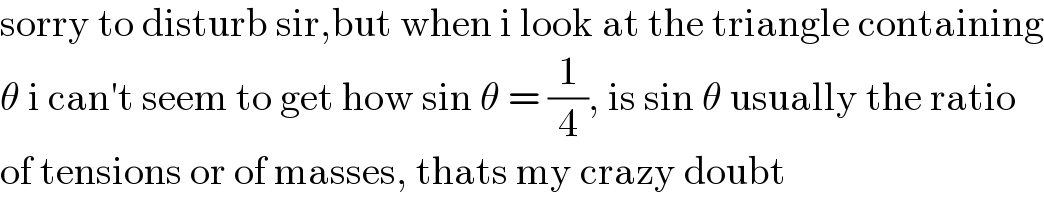
$$\mathrm{sorry}\:\mathrm{to}\:\mathrm{disturb}\:\mathrm{sir},\mathrm{but}\:\mathrm{when}\:\mathrm{i}\:\mathrm{look}\:\mathrm{at}\:\mathrm{the}\:\mathrm{triangle}\:\mathrm{containing} \\ $$$$\theta\:\mathrm{i}\:\mathrm{can}'\mathrm{t}\:\mathrm{seem}\:\mathrm{to}\:\mathrm{get}\:\mathrm{how}\:\mathrm{sin}\:\theta\:=\:\frac{\mathrm{1}}{\mathrm{4}},\:\mathrm{is}\:\mathrm{sin}\:\theta\:\mathrm{usually}\:\mathrm{the}\:\mathrm{ratio} \\ $$$$\mathrm{of}\:\mathrm{tensions}\:\mathrm{or}\:\mathrm{of}\:\mathrm{masses},\:\mathrm{thats}\:\mathrm{my}\:\mathrm{crazy}\:\mathrm{doubt} \\ $$
Commented by mr W last updated on 06/Apr/21
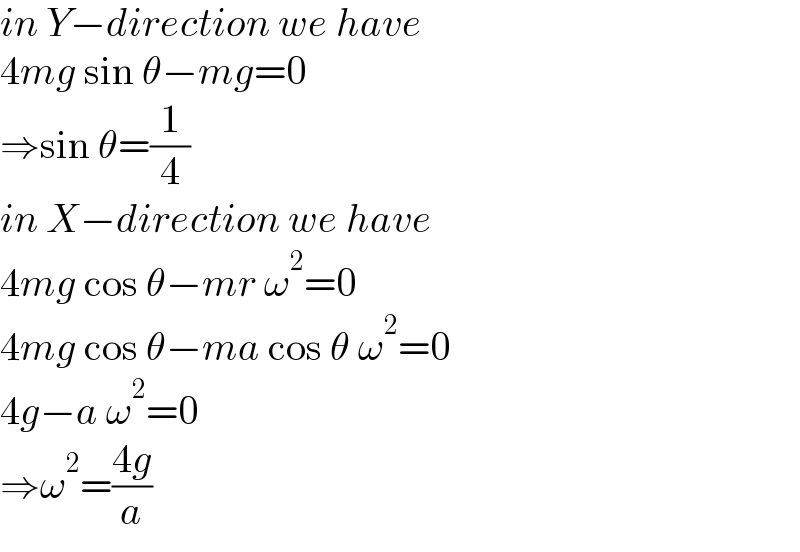
$${in}\:{Y}−{direction}\:{we}\:{have} \\ $$$$\mathrm{4}{mg}\:\mathrm{sin}\:\theta−{mg}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{sin}\:\theta=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${in}\:{X}−{direction}\:{we}\:{have} \\ $$$$\mathrm{4}{mg}\:\mathrm{cos}\:\theta−{mr}\:\omega^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{4}{mg}\:\mathrm{cos}\:\theta−{ma}\:\mathrm{cos}\:\theta\:\omega^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{4}{g}−{a}\:\omega^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\omega^{\mathrm{2}} =\frac{\mathrm{4}{g}}{{a}} \\ $$
Commented by physicstutes last updated on 06/Apr/21
$$\mathrm{wow}\:\mathrm{i}\:\mathrm{get}\:\mathrm{nicely}\:\mathrm{now}.\:\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}\: \\ $$
