
Question Number 137588 by bramlexs22 last updated on 04/Apr/21
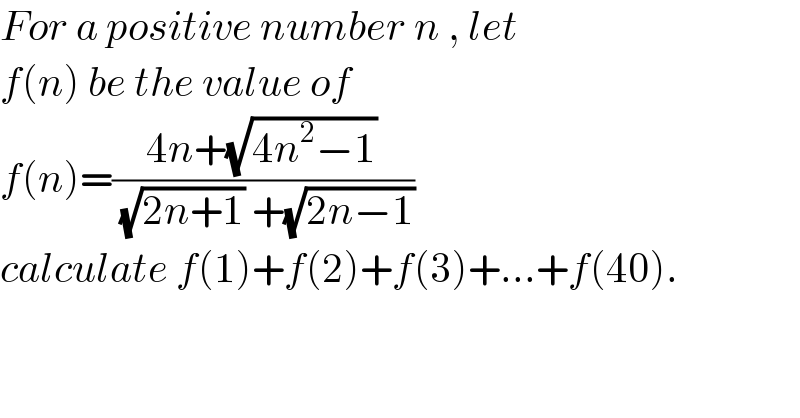
$${For}\:{a}\:{positive}\:{number}\:{n}\:,\:{let} \\ $$$${f}\left({n}\right)\:{be}\:{the}\:{value}\:{of}\: \\ $$$${f}\left({n}\right)=\frac{\mathrm{4}{n}+\sqrt{\mathrm{4}{n}^{\mathrm{2}} −\mathrm{1}}}{\:\sqrt{\mathrm{2}{n}+\mathrm{1}}\:+\sqrt{\mathrm{2}{n}−\mathrm{1}}} \\ $$$${calculate}\:{f}\left(\mathrm{1}\right)+{f}\left(\mathrm{2}\right)+{f}\left(\mathrm{3}\right)+...+{f}\left(\mathrm{40}\right). \\ $$
Answered by bemath last updated on 04/Apr/21
![⇔ f(n)=((((√(2n+1)))^2 +((√(2n−1)))^2 +(√((2n+1)(2n−1))))/( (√(2n+1)) +(√(2n−1)))) f(n)= ((((√(2n+1)) )^3 −((√(2n−1)) )^3 )/2) f(1)+f(2)+f(3)+...+f(40) = (((√3^3 )−(√1^3 ))/2) + (((√5^3 )−(√3^3 ))/2) + (((√7^3 )−(√5^3 ))/2) +...+ (((√(81^3 ))−(√(79^3 )))/2) [ telescopy series ] f(1)+f(2)+f(3)+...+f(40) = (((√(81^3 ))−(√1^3 ))/2) = ((9^3 −1)/2) = ((728)/2) = 364](Q137595.png)
$$\Leftrightarrow\:{f}\left({n}\right)=\frac{\left(\sqrt{\mathrm{2}{n}+\mathrm{1}}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{2}{n}−\mathrm{1}}\right)^{\mathrm{2}} +\sqrt{\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{2}{n}−\mathrm{1}\right)}}{\:\sqrt{\mathrm{2}{n}+\mathrm{1}}\:+\sqrt{\mathrm{2}{n}−\mathrm{1}}} \\ $$$${f}\left({n}\right)=\:\frac{\left(\sqrt{\mathrm{2}{n}+\mathrm{1}}\:\right)^{\mathrm{3}} −\left(\sqrt{\mathrm{2}{n}−\mathrm{1}}\:\right)^{\mathrm{3}} }{\mathrm{2}} \\ $$$${f}\left(\mathrm{1}\right)+{f}\left(\mathrm{2}\right)+{f}\left(\mathrm{3}\right)+...+{f}\left(\mathrm{40}\right) \\ $$$$=\:\frac{\sqrt{\mathrm{3}^{\mathrm{3}} }−\sqrt{\mathrm{1}^{\mathrm{3}} }}{\mathrm{2}}\:+\:\frac{\sqrt{\mathrm{5}^{\mathrm{3}} }−\sqrt{\mathrm{3}^{\mathrm{3}} }}{\mathrm{2}}\:+\:\frac{\sqrt{\mathrm{7}^{\mathrm{3}} }−\sqrt{\mathrm{5}^{\mathrm{3}} }}{\mathrm{2}}\:+...+\:\frac{\sqrt{\mathrm{81}^{\mathrm{3}} }−\sqrt{\mathrm{79}^{\mathrm{3}} }}{\mathrm{2}} \\ $$$$\left[\:{telescopy}\:{series}\:\right] \\ $$$${f}\left(\mathrm{1}\right)+{f}\left(\mathrm{2}\right)+{f}\left(\mathrm{3}\right)+...+{f}\left(\mathrm{40}\right) \\ $$$$=\:\frac{\sqrt{\mathrm{81}^{\mathrm{3}} }−\sqrt{\mathrm{1}^{\mathrm{3}} }}{\mathrm{2}}\:=\:\frac{\mathrm{9}^{\mathrm{3}} −\mathrm{1}}{\mathrm{2}}\:=\:\frac{\mathrm{728}}{\mathrm{2}}\:=\:\mathrm{364}\: \\ $$
