
Question Number 137585 by bramlexs22 last updated on 04/Apr/21
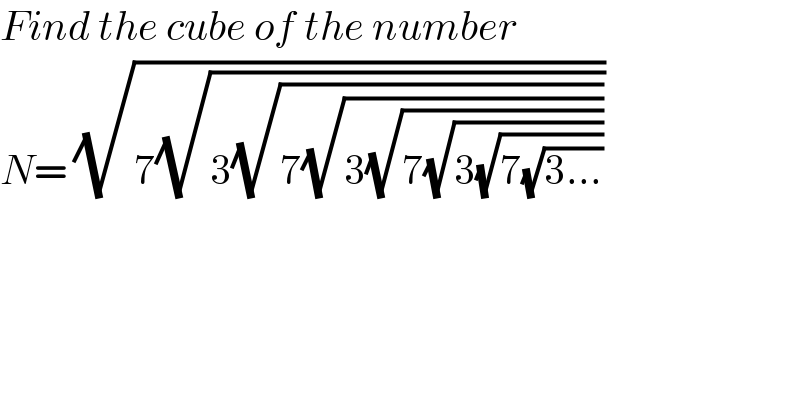
$${Find}\:{the}\:{cube}\:{of}\:{the}\:{number}\: \\ $$$${N}=\:\sqrt{\mathrm{7}\sqrt{\mathrm{3}\sqrt{\mathrm{7}\sqrt{\mathrm{3}\sqrt{\mathrm{7}\sqrt{\mathrm{3}\sqrt{\mathrm{7}\sqrt{\mathrm{3}...}}}}}}}} \\ $$
Answered by bemath last updated on 04/Apr/21
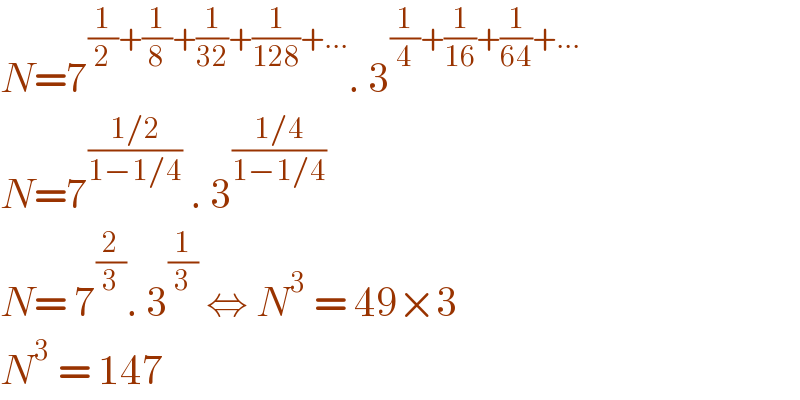
$${N}=\mathrm{7}^{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{32}}+\frac{\mathrm{1}}{\mathrm{128}}+...} .\:\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{16}}+\frac{\mathrm{1}}{\mathrm{64}}+...} \\ $$$${N}=\mathrm{7}^{\frac{\mathrm{1}/\mathrm{2}}{\mathrm{1}−\mathrm{1}/\mathrm{4}}} \:.\:\mathrm{3}^{\frac{\mathrm{1}/\mathrm{4}}{\mathrm{1}−\mathrm{1}/\mathrm{4}}} \\ $$$${N}=\:\mathrm{7}^{\frac{\mathrm{2}}{\mathrm{3}}} .\:\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{3}}} \:\Leftrightarrow\:{N}^{\mathrm{3}} \:=\:\mathrm{49}×\mathrm{3} \\ $$$${N}^{\mathrm{3}} \:=\:\mathrm{147} \\ $$
Answered by mr W last updated on 04/Apr/21
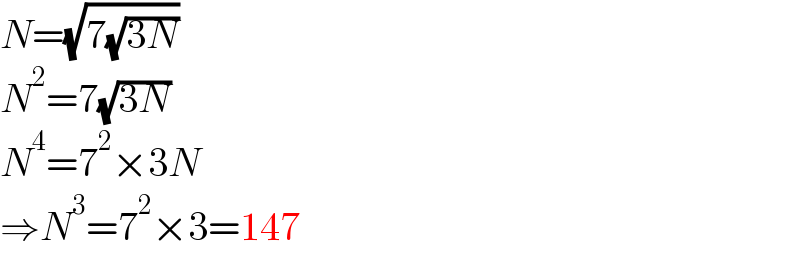
$${N}=\sqrt{\mathrm{7}\sqrt{\mathrm{3}{N}}} \\ $$$${N}^{\mathrm{2}} =\mathrm{7}\sqrt{\mathrm{3}{N}} \\ $$$${N}^{\mathrm{4}} =\mathrm{7}^{\mathrm{2}} ×\mathrm{3}{N} \\ $$$$\Rightarrow{N}^{\mathrm{3}} =\mathrm{7}^{\mathrm{2}} ×\mathrm{3}=\mathrm{147} \\ $$
