
Question Number 13751 by Nayon last updated on 23/May/17
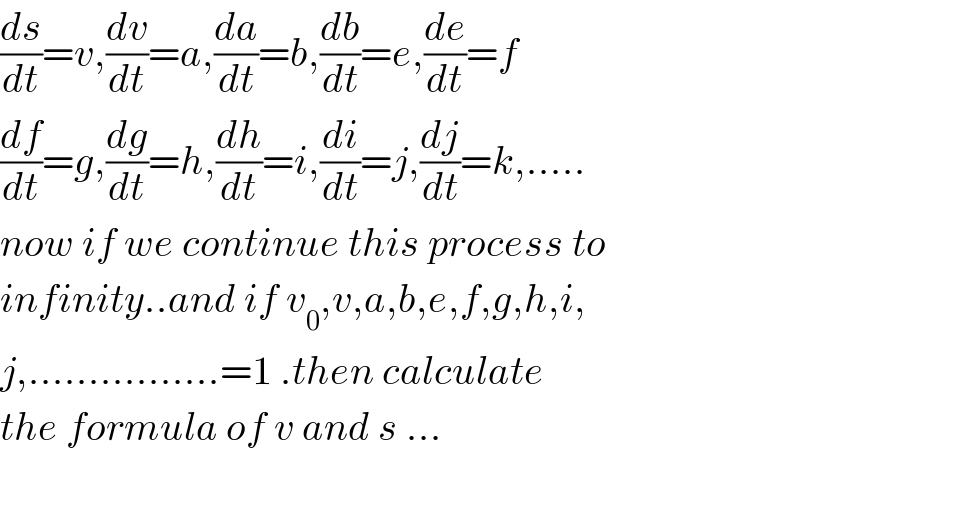
$$\frac{{ds}}{{dt}}={v},\frac{{dv}}{{dt}}={a},\frac{{da}}{{dt}}={b},\frac{{db}}{{dt}}={e},\frac{{de}}{{dt}}={f} \\ $$$$\frac{{df}}{{dt}}={g},\frac{{dg}}{{dt}}={h},\frac{{dh}}{{dt}}={i},\frac{{di}}{{dt}}={j},\frac{{dj}}{{dt}}={k},..... \\ $$$${now}\:{if}\:{we}\:{continue}\:{this}\:{process}\:{to} \\ $$$${infinity}..{and}\:{if}\:{v}_{\mathrm{0}} ,{v},{a},{b},{e},{f},{g},{h},{i}, \\ $$$${j},................=\mathrm{1}\:.{then}\:{calculate} \\ $$$${the}\:{formula}\:{of}\:{v}\:{and}\:{s}\:... \\ $$$$ \\ $$
Commented by ajfour last updated on 23/May/17

$${s}={v}=\boldsymbol{{e}}^{\boldsymbol{{t}}} \\ $$
Commented by Nayon last updated on 23/May/17

$${detAils} \\ $$
Commented by Nayon last updated on 23/May/17

$${v}={e}^{{t}} \:{right}\:{but} \\ $$$${s}={e}^{{t}} −\mathrm{1} \\ $$$$ \\ $$
Commented by ajfour last updated on 23/May/17

$${agree} \\ $$
Answered by ajfour last updated on 23/May/17
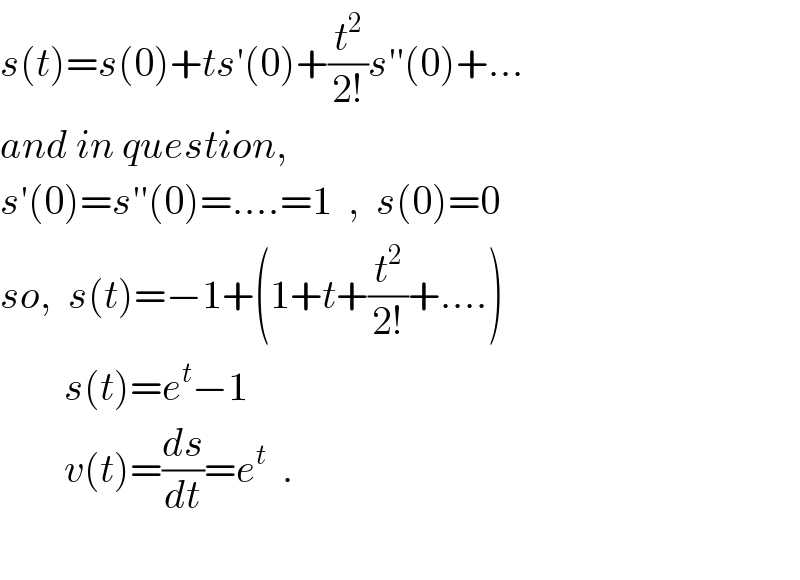
$${s}\left({t}\right)={s}\left(\mathrm{0}\right)+{ts}'\left(\mathrm{0}\right)+\frac{{t}^{\mathrm{2}} }{\mathrm{2}!}{s}''\left(\mathrm{0}\right)+... \\ $$$${and}\:{in}\:{question}, \\ $$$${s}'\left(\mathrm{0}\right)={s}''\left(\mathrm{0}\right)=....=\mathrm{1}\:\:,\:\:{s}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$${so},\:\:{s}\left({t}\right)=−\mathrm{1}+\left(\mathrm{1}+{t}+\frac{{t}^{\mathrm{2}} }{\mathrm{2}!}+....\right) \\ $$$$\:\:\:\:\:\:\:\:{s}\left({t}\right)={e}^{{t}} −\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:{v}\left({t}\right)=\frac{{ds}}{{dt}}={e}^{{t}} \:\:. \\ $$$$ \\ $$
Commented by Nayon last updated on 24/May/17

$${Has}\:{there}\:{any}\:{object}\:{in}\:{the}\: \\ $$$${universe}\:{which}\:{adhere}\:{this}\:{formula}? \\ $$
