Question and Answers Forum

All Question   Topic List

Question Number 136006 by liberty last updated on 17/Mar/21

$$ \\ $$ What are the dimensions of the rectangle of maximum area that can be inscribed in the portion of the parabola x^2=8y intercepted by the line y=2?\\n

Answered by mr W last updated on 18/Mar/21

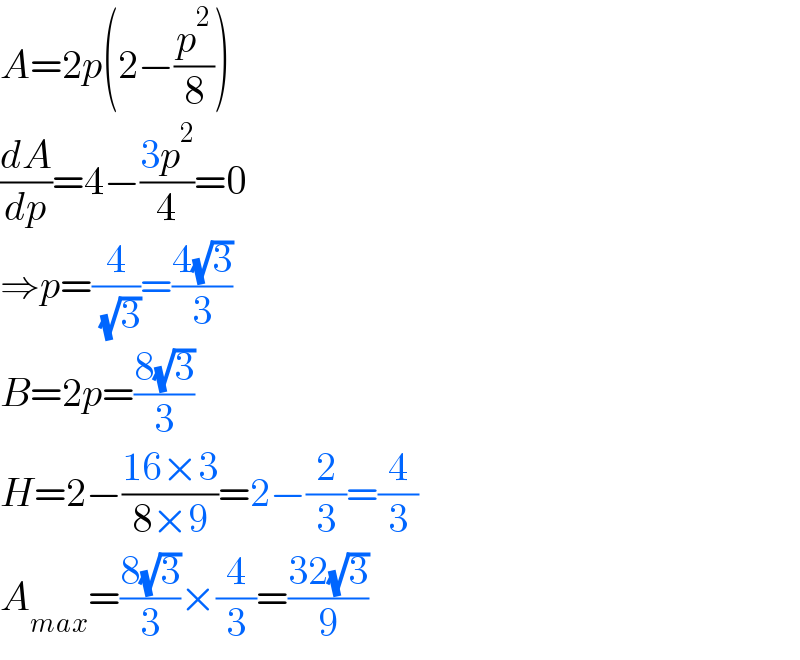
A=2p(2−(p^2 /8)) (dA/dp)=4−((3p^2 )/4)=0 ⇒p=(4/( (√3)))=((4(√3))/3) B=2p=((8(√3))/3) H=2−((16×3)/(8×9))=2−(2/3)=(4/3) A_(max) =((8(√3))/3)×(4/3)=((32(√3))/9)

$${A}=\mathrm{2}{p}\left(\mathrm{2}−\frac{{p}^{\mathrm{2}} }{\mathrm{8}}\right) \\ $$ $$\frac{{dA}}{{dp}}=\mathrm{4}−\frac{\mathrm{\color{mathblue}{3}}{p}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{0} \\ $$ $$\Rightarrow{p}=\frac{\mathrm{\color{mathblue}{4}}}{\:\sqrt{\mathrm{\color{mathblue}{3}}}}\color{mathblue}{=}\frac{\mathrm{\color{mathblue}{4}}\sqrt{\mathrm{\color{mathblue}{3}}}}{\mathrm{\color{mathblue}{3}}} \\ $$ $${B}=\mathrm{2}{p}=\frac{\mathrm{\color{mathblue}{8}}\sqrt{\mathrm{\color{mathblue}{3}}}}{\mathrm{\color{mathblue}{3}}} \\ $$ $${H}=\mathrm{2}−\frac{\mathrm{\color{mathblue}{1}\color{mathblue}{6}}\color{mathblue}{×}\mathrm{\color{mathblue}{3}}}{\mathrm{8}\color{mathblue}{×}\mathrm{\color{mathblue}{9}}}=\mathrm{\color{mathblue}{2}}\color{mathblue}{−}\frac{\mathrm{\color{mathblue}{2}}}{\mathrm{\color{mathblue}{3}}}\color{mathblue}{=}\frac{\mathrm{\color{mathblue}{4}}}{\mathrm{\color{mathblue}{3}}} \\ $$ $${A}_{{max}} =\frac{\mathrm{\color{mathblue}{8}}\sqrt{\mathrm{\color{mathblue}{3}}}}{\mathrm{\color{mathblue}{3}}}\color{mathblue}{×}\frac{\mathrm{\color{mathblue}{4}}}{\mathrm{\color{mathblue}{3}}}=\frac{\mathrm{\color{mathblue}{3}\color{mathblue}{2}}\sqrt{\mathrm{\color{mathblue}{3}}}}{\mathrm{\color{mathblue}{9}}} \\ $$

Commented byotchereabdullai@gmail.com last updated on 17/Mar/21

nice!

$$\mathrm{nice}! \\ $$

Commented byliberty last updated on 17/Mar/21

i got ((32)/(3(√3))) sir

$${i}\:{got}\:\frac{\mathrm{32}}{\mathrm{3}\sqrt{\mathrm{3}}}\:{sir} \\ $$

Commented byliberty last updated on 18/Mar/21

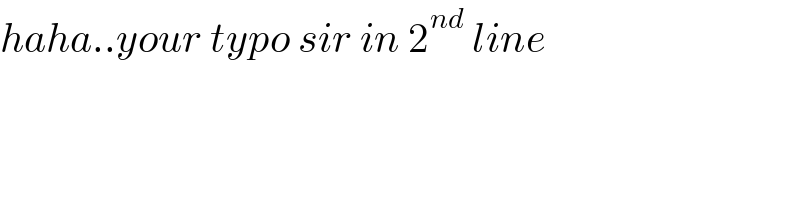
haha..your typo sir in 2^(nd) line

$${haha}..{your}\:{typo}\:{sir}\:{in}\:\mathrm{2}^{{nd}} \:{line} \\ $$

Commented bymr W last updated on 18/Mar/21

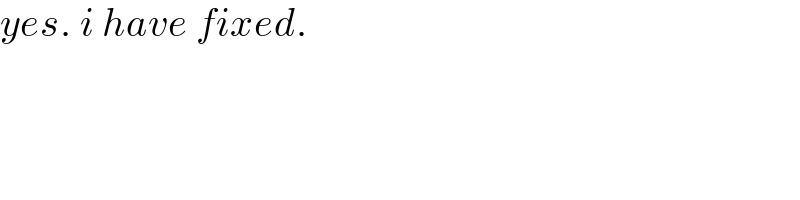
yes. i have fixed.

$${yes}.\:{i}\:{have}\:{fixed}. \\ $$

Answered by liberty last updated on 17/Mar/21

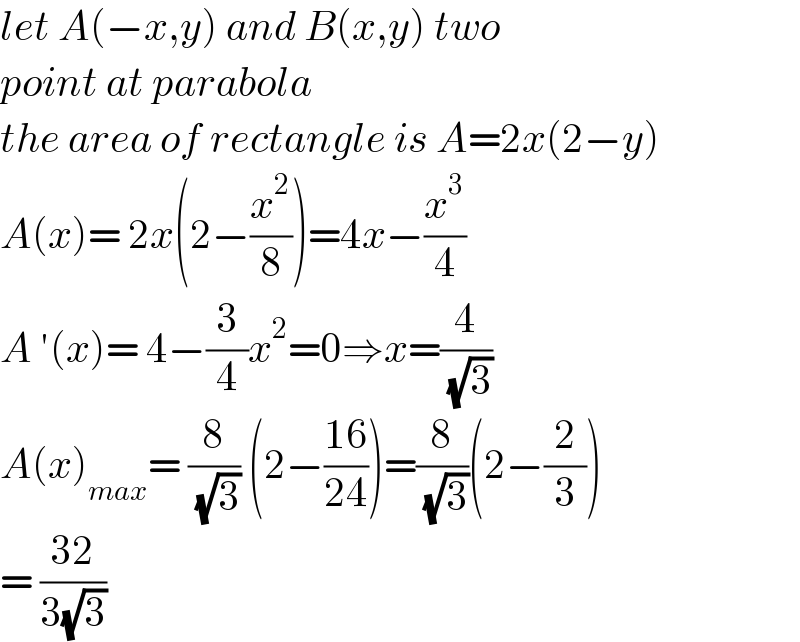
let A(−x,y) and B(x,y) two point at parabola the area of rectangle is A=2x(2−y) A(x)= 2x(2−(x^2 /8))=4x−(x^3 /4) A ′(x)= 4−(3/4)x^2 =0⇒x=(4/( (√3))) A(x)_(max) = (8/( (√3))) (2−((16)/(24)))=(8/( (√3)))(2−(2/3)) = ((32)/(3(√3)))

$${let}\:{A}\left(−{x},{y}\right)\:{and}\:{B}\left({x},{y}\right)\:{two} \\ $$ $${point}\:{at}\:{parabola}\: \\ $$ $${the}\:{area}\:{of}\:{rectangle}\:{is}\:{A}=\mathrm{2}{x}\left(\mathrm{2}−{y}\right) \\ $$ $${A}\left({x}\right)=\:\mathrm{2}{x}\left(\mathrm{2}−\frac{{x}^{\mathrm{2}} }{\mathrm{8}}\right)=\mathrm{4}{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{4}} \\ $$ $${A}\:'\left({x}\right)=\:\mathrm{4}−\frac{\mathrm{3}}{\mathrm{4}}{x}^{\mathrm{2}} =\mathrm{0}\Rightarrow{x}=\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}} \\ $$ $${A}\left({x}\right)_{{max}} =\:\frac{\mathrm{8}}{\:\sqrt{\mathrm{3}}}\:\left(\mathrm{2}−\frac{\mathrm{16}}{\mathrm{24}}\right)=\frac{\mathrm{8}}{\:\sqrt{\mathrm{3}}}\left(\mathrm{2}−\frac{\mathrm{2}}{\mathrm{3}}\right) \\ $$ $$=\:\frac{\mathrm{32}}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com