
Question Number 135679 by liberty last updated on 15/Mar/21
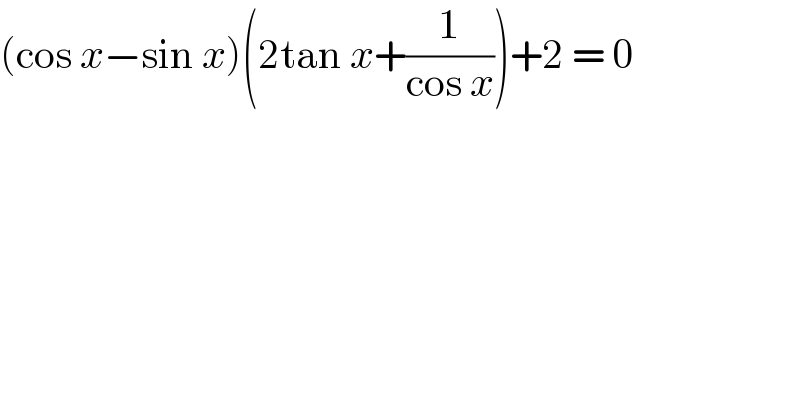
$$\left(\mathrm{cos}\:{x}−\mathrm{sin}\:{x}\right)\left(\mathrm{2tan}\:{x}+\frac{\mathrm{1}}{\mathrm{cos}\:{x}}\right)+\mathrm{2}\:=\:\mathrm{0} \\ $$
Answered by EDWIN88 last updated on 15/Mar/21

$$\mathrm{Let}\:\mathrm{tan}\:\frac{\mathrm{x}}{\mathrm{2}}\:=\:\mathrm{t}\:\rightarrow\begin{cases}{\mathrm{cos}\:\mathrm{x}=\frac{\mathrm{1}−\mathrm{t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}\\{\mathrm{sin}\:\mathrm{x}=\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}\\{\mathrm{tan}\:\mathrm{x}=\frac{\mathrm{2t}}{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }}\end{cases} \\ $$$$\Leftrightarrow\:\left(\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }−\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right)\left(\frac{\mathrm{4t}}{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }+\frac{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }{\mathrm{1}−\mathrm{t}}\right)+\mathrm{2}\:=\:\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} −\mathrm{2t}\right).\left(\mathrm{t}^{\mathrm{2}} +\mathrm{4t}+\mathrm{1}\right)+\mathrm{2}\left(\mathrm{1}−\mathrm{t}^{\mathrm{4}} \right)\:=\:\mathrm{0} \\ $$$$\Rightarrow\mathrm{3t}^{\mathrm{4}} −\mathrm{t}^{\mathrm{2}} +\mathrm{6t}^{\mathrm{3}} −\mathrm{2t}+\mathrm{9t}^{\mathrm{2}} −\mathrm{3}\:=\:\mathrm{0} \\ $$$$\Rightarrow\mathrm{t}^{\mathrm{2}} \left(\mathrm{3t}^{\mathrm{2}} −\mathrm{1}\right)+\mathrm{2t}\left(\mathrm{3t}^{\mathrm{2}} −\mathrm{1}\right)+\mathrm{3}\left(\mathrm{3t}^{\mathrm{2}} −\mathrm{1}\right)\:=\:\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{3t}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} +\mathrm{2t}+\mathrm{3}\right)\:=\:\mathrm{0} \\ $$$$\:\begin{cases}{\mathrm{t}^{\mathrm{2}} +\mathrm{2t}+\mathrm{3}\:=\:\mathrm{0}\:\rightarrow\mathrm{has}\:\mathrm{complex}\:\mathrm{roots}}\\{\mathrm{3t}^{\mathrm{2}} −\mathrm{1}=\mathrm{0}\Rightarrow\mathrm{t}\:=\:\pm\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}}\end{cases} \\ $$$$\Leftrightarrow\:\mathrm{tan}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\:=\:\pm\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:;\:\frac{\mathrm{x}}{\mathrm{2}}\:=\:\mathrm{n}\pi\:\pm\:\frac{\pi}{\mathrm{6}} \\ $$$$\Rightarrow\:\mathrm{x}\:=\:\mathrm{2n}\pi\:\pm\:\frac{\pi}{\mathrm{3}}\:;\:\mathrm{n}\in\mathbb{Z} \\ $$$$ \\ $$
