
Previous in Relation and Functions Next in Relation and Functions
Question Number 135378 by Bird last updated on 12/Mar/21
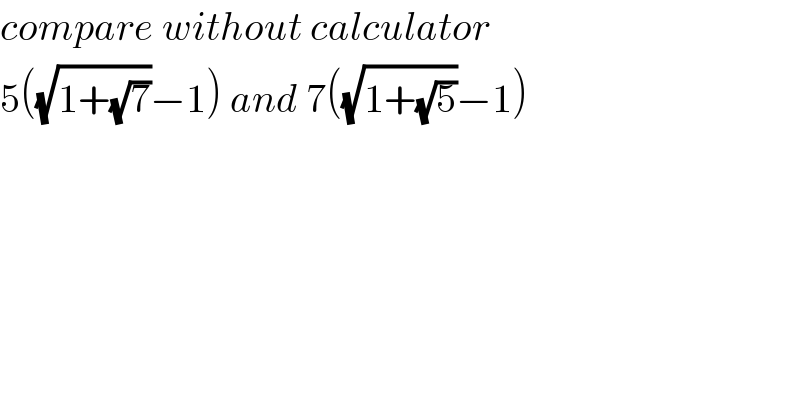
$${compare}\:{without}\:{calculator} \\ $$$$\mathrm{5}\left(\sqrt{\mathrm{1}+\sqrt{\mathrm{7}}}−\mathrm{1}\right)\:{and}\:\mathrm{7}\left(\sqrt{\mathrm{1}+\sqrt{\mathrm{5}}}−\mathrm{1}\right) \\ $$
Answered by mr W last updated on 12/Mar/21
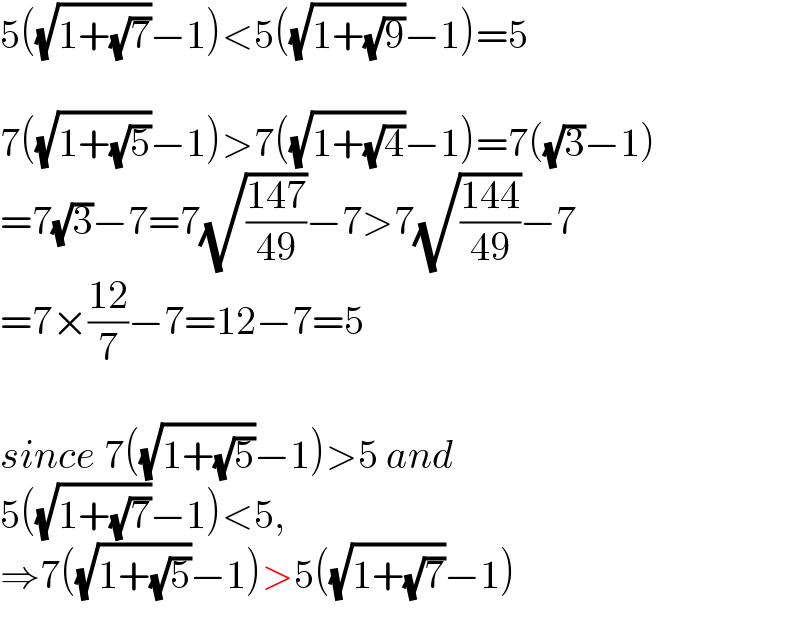
$$\mathrm{5}\left(\sqrt{\mathrm{1}+\sqrt{\mathrm{7}}}−\mathrm{1}\right)<\mathrm{5}\left(\sqrt{\mathrm{1}+\sqrt{\mathrm{9}}}−\mathrm{1}\right)=\mathrm{5} \\ $$$$ \\ $$$$\mathrm{7}\left(\sqrt{\mathrm{1}+\sqrt{\mathrm{5}}}−\mathrm{1}\right)>\mathrm{7}\left(\sqrt{\mathrm{1}+\sqrt{\mathrm{4}}}−\mathrm{1}\right)=\mathrm{7}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right) \\ $$$$=\mathrm{7}\sqrt{\mathrm{3}}−\mathrm{7}=\mathrm{7}\sqrt{\frac{\mathrm{147}}{\mathrm{49}}}−\mathrm{7}>\mathrm{7}\sqrt{\frac{\mathrm{144}}{\mathrm{49}}}−\mathrm{7} \\ $$$$=\mathrm{7}×\frac{\mathrm{12}}{\mathrm{7}}−\mathrm{7}=\mathrm{12}−\mathrm{7}=\mathrm{5} \\ $$$$ \\ $$$${since}\:\mathrm{7}\left(\sqrt{\mathrm{1}+\sqrt{\mathrm{5}}}−\mathrm{1}\right)>\mathrm{5}\:{and} \\ $$$$\mathrm{5}\left(\sqrt{\mathrm{1}+\sqrt{\mathrm{7}}}−\mathrm{1}\right)<\mathrm{5}, \\ $$$$\Rightarrow\mathrm{7}\left(\sqrt{\mathrm{1}+\sqrt{\mathrm{5}}}−\mathrm{1}\right)>\mathrm{5}\left(\sqrt{\mathrm{1}+\sqrt{\mathrm{7}}}−\mathrm{1}\right) \\ $$
Commented by mathmax by abdo last updated on 12/Mar/21

$$\mathrm{thankx}\:\mathrm{sir}\:\mathrm{mrw} \\ $$
