
Question Number 135172 by bemath last updated on 11/Mar/21
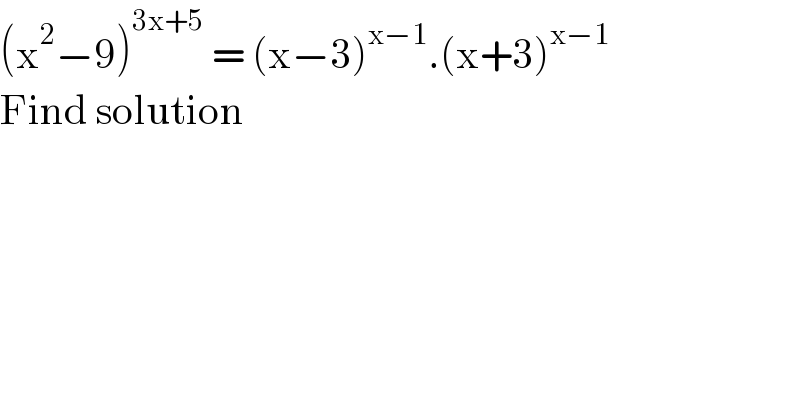
$$\left(\mathrm{x}^{\mathrm{2}} −\mathrm{9}\right)^{\mathrm{3x}+\mathrm{5}} \:=\:\left(\mathrm{x}−\mathrm{3}\right)^{\mathrm{x}−\mathrm{1}} .\left(\mathrm{x}+\mathrm{3}\right)^{\mathrm{x}−\mathrm{1}} \\ $$$$\mathrm{Find}\:\mathrm{solution} \\ $$
Answered by john_santu last updated on 11/Mar/21

$$\Rightarrow\left({x}^{\mathrm{2}} −\mathrm{9}\right)^{\mathrm{3}{x}+\mathrm{5}} \:=\:\left({x}^{\mathrm{2}} −\mathrm{9}\right)^{{x}−\mathrm{1}} \\ $$$${case}\left(\mathrm{1}\right)\:\mathrm{3}{x}+\mathrm{5}\:=\:{x}−\mathrm{1}\:;\:{x}=−\mathrm{3}\: \\ $$$${checking}\:{solution}\:\left(\mathrm{0}\right)^{−\mathrm{4}} \:=\:\infty\: \\ $$$${so}\:{x}=−\mathrm{3}\:{no}\:{solution} \\ $$$${case}\left(\mathrm{2}\right)\:{x}^{\mathrm{2}} −\mathrm{9}\:=\:\mathrm{1}\:;\:{x}\:=\:\pm\:\sqrt{\mathrm{10}}\:{solution} \\ $$$${case}\left(\mathrm{3}\right)\:{x}^{\mathrm{2}} −\mathrm{9}\:=\:\mathrm{0}\:,\:{x}\:=\:\mathrm{3}\:,\:{since}\:{x}=−\mathrm{3}\left({rejected}\right) \\ $$$${case}\left(\mathrm{4}\right)\:{x}^{\mathrm{2}} −\mathrm{9}\:=−\mathrm{1}\:;\:{x}\:=\:\pm\mathrm{2}\sqrt{\mathrm{2}} \\ $$$${cheking}\:{solution}\: \\ $$$$\begin{cases}{\left(−\mathrm{1}\right)^{\mathrm{6}\sqrt{\mathrm{2}}+\mathrm{5}} \:\approx\:−\mathrm{0}.\mathrm{0462}}\\{\left(−\mathrm{1}\right)^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\approx\:\mathrm{0}.\mathrm{266}}\end{cases}\:{no}\:{solution} \\ $$$$\begin{cases}{\left(−\mathrm{1}\right)^{−\mathrm{6}\sqrt{\mathrm{2}}+\mathrm{5}} \:\approx\:−\mathrm{0}.\mathrm{0462}}\\{\left(−\mathrm{1}\right)^{−\sqrt{\mathrm{2}}−\mathrm{1}} \:\approx\:\mathrm{0}.\mathrm{266}}\end{cases}{no}\:{solution} \\ $$$$\therefore\:{the}\:{solution}\:{is}\:\left\{\:\mathrm{3};\:\pm\:\sqrt{\mathrm{10}}\:\right\}\: \\ $$$$ \\ $$
Commented by metamorfose last updated on 11/Mar/21

$${why}\:−\mathrm{3}\:{isn}'{t}\:{a}\:{solution}?... \\ $$
Answered by metamorfose last updated on 11/Mar/21
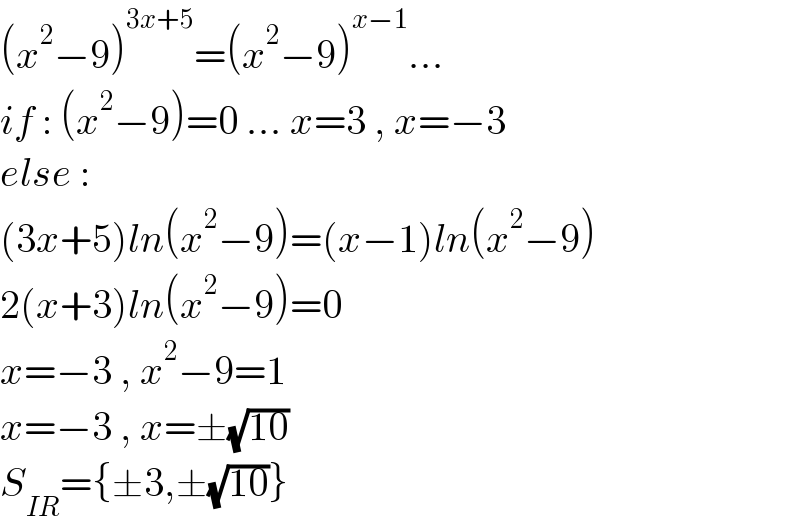
$$\left({x}^{\mathrm{2}} −\mathrm{9}\right)^{\mathrm{3}{x}+\mathrm{5}} =\left({x}^{\mathrm{2}} −\mathrm{9}\right)^{{x}−\mathrm{1}} ... \\ $$$${if}\::\:\left({x}^{\mathrm{2}} −\mathrm{9}\right)=\mathrm{0}\:...\:{x}=\mathrm{3}\:,\:{x}=−\mathrm{3}\: \\ $$$${else}\:: \\ $$$$\left(\mathrm{3}{x}+\mathrm{5}\right){ln}\left({x}^{\mathrm{2}} −\mathrm{9}\right)=\left({x}−\mathrm{1}\right){ln}\left({x}^{\mathrm{2}} −\mathrm{9}\right) \\ $$$$\mathrm{2}\left({x}+\mathrm{3}\right){ln}\left({x}^{\mathrm{2}} −\mathrm{9}\right)=\mathrm{0} \\ $$$${x}=−\mathrm{3}\:,\:{x}^{\mathrm{2}} −\mathrm{9}=\mathrm{1} \\ $$$${x}=−\mathrm{3}\:,\:{x}=\pm\sqrt{\mathrm{10}} \\ $$$${S}_{{IR}} =\left\{\pm\mathrm{3},\pm\sqrt{\mathrm{10}}\right\} \\ $$
