
Question Number 134981 by oooooooo last updated on 09/Mar/21
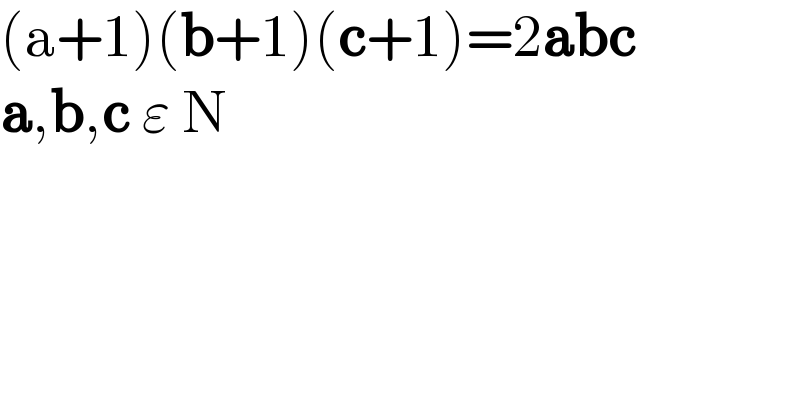
$$\left(\mathrm{a}+\mathrm{1}\right)\left(\boldsymbol{\mathrm{b}}+\mathrm{1}\right)\left(\boldsymbol{\mathrm{c}}+\mathrm{1}\right)=\mathrm{2}\boldsymbol{\mathrm{abc}}\: \\ $$$$\boldsymbol{\mathrm{a}},\boldsymbol{\mathrm{b}},\boldsymbol{\mathrm{c}}\:\varepsilon\:\mathrm{N} \\ $$
Answered by MJS_new last updated on 10/Mar/21
![let a≤b≤c (1) c=(a+1)(b+1) ⇒ b=((a+2)/(a−1))∧c=(((a+1)(2a+1))/(a−1)) a=2∧b=4∧c=15 (2) ab=c+1 ⇒ b=((a+3)/(a−1))∧c=(((a+1)^2 )/(a−1)) a=2∧b=5∧c=9 a=b=3∧c=8 (3) bc=(a+1)(b+1) ⇒ b=((a+1)/(a−2))∧c=2a−1 a=3∧b=4∧c=5 (4) b=2a+2∧c=2a+3 ⇔ c=b+1∧2b=c+1 [the idea here is to get an additional factor 2 on the lhs] a=2∧b=6∧c=7](Q135074.png)
$$\mathrm{let}\:{a}\leqslant{b}\leqslant{c} \\ $$$$\left(\mathrm{1}\right)\:{c}=\left({a}+\mathrm{1}\right)\left({b}+\mathrm{1}\right) \\ $$$$\:\:\:\:\:\Rightarrow\:{b}=\frac{{a}+\mathrm{2}}{{a}−\mathrm{1}}\wedge{c}=\frac{\left({a}+\mathrm{1}\right)\left(\mathrm{2}{a}+\mathrm{1}\right)}{{a}−\mathrm{1}} \\ $$$$\:\:\:\:\:{a}=\mathrm{2}\wedge{b}=\mathrm{4}\wedge{c}=\mathrm{15} \\ $$$$\left(\mathrm{2}\right)\:{ab}={c}+\mathrm{1} \\ $$$$\:\:\:\:\:\Rightarrow\:{b}=\frac{{a}+\mathrm{3}}{{a}−\mathrm{1}}\wedge{c}=\frac{\left({a}+\mathrm{1}\right)^{\mathrm{2}} }{{a}−\mathrm{1}} \\ $$$$\:\:\:\:\:{a}=\mathrm{2}\wedge{b}=\mathrm{5}\wedge{c}=\mathrm{9} \\ $$$$\:\:\:\:\:{a}={b}=\mathrm{3}\wedge{c}=\mathrm{8} \\ $$$$\left(\mathrm{3}\right)\:{bc}=\left({a}+\mathrm{1}\right)\left({b}+\mathrm{1}\right) \\ $$$$\:\:\:\:\:\Rightarrow\:{b}=\frac{{a}+\mathrm{1}}{{a}−\mathrm{2}}\wedge{c}=\mathrm{2}{a}−\mathrm{1} \\ $$$$\:\:\:\:\:{a}=\mathrm{3}\wedge{b}=\mathrm{4}\wedge{c}=\mathrm{5} \\ $$$$\left(\mathrm{4}\right)\:{b}=\mathrm{2}{a}+\mathrm{2}\wedge{c}=\mathrm{2}{a}+\mathrm{3}\:\Leftrightarrow\:{c}={b}+\mathrm{1}\wedge\mathrm{2}{b}={c}+\mathrm{1} \\ $$$$\:\:\:\:\:\left[\mathrm{the}\:\mathrm{idea}\:\mathrm{here}\:\mathrm{is}\:\mathrm{to}\:\mathrm{get}\:\mathrm{an}\:\mathrm{additional}\right. \\ $$$$\left.\:\:\:\:\:\:\mathrm{factor}\:\mathrm{2}\:\mathrm{on}\:\mathrm{the}\:\mathrm{lhs}\right] \\ $$$$\:\:\:\:\:{a}=\mathrm{2}\wedge{b}=\mathrm{6}\wedge{c}=\mathrm{7} \\ $$
