Question Number 134905 by bramlexs22 last updated on 08/Mar/21

$$\mathrm{Combinatorics} \\ $$ What is the number of ways of distributing 9 different objects among 5 persons such that each gets at least 1?\\n
Commented bysoumyasaha last updated on 08/Mar/21
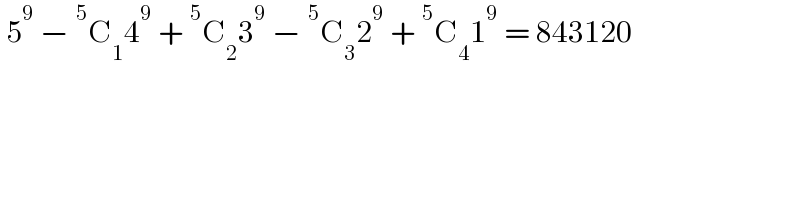
$$\:\mathrm{5}^{\mathrm{9}} \:−\:^{\mathrm{5}} \mathrm{C}_{\mathrm{1}} \mathrm{4}^{\mathrm{9}} \:+\:^{\mathrm{5}} \mathrm{C}_{\mathrm{2}} \mathrm{3}^{\mathrm{9}} \:−\:^{\mathrm{5}} \mathrm{C}_{\mathrm{3}} \mathrm{2}^{\mathrm{9}} \:+\:^{\mathrm{5}} \mathrm{C}_{\mathrm{4}} \mathrm{1}^{\mathrm{9}} \:=\:\mathrm{843120} \\ $$
Answered by math55 last updated on 08/Mar/21

$$\underline{{Solution}} \\ $$ $${Given}, \\ $$ $$\:{Total}\:{objects}\:'{n}'=\mathrm{9} \\ $$ $$\:{Total}\:{person}\:'{r}'=\mathrm{5} \\ $$ $${then}, \\ $$ $${Total}\:{way}\:{for}\:{the}=^{{n}} {P}_{{r}} \\ $$ $${distribution} \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=^{\mathrm{9}} {P}_{\mathrm{5}} =\frac{\mathrm{9}!}{\left(\mathrm{9}−\mathrm{5}\right)!} \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{9}!}{\mathrm{4}!} \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[\:\:\:=\mathrm{15120}\:{ways}\right. \\ $$
Commented bybramlexs22 last updated on 08/Mar/21

$$\mathrm{wrong} \\ $$
Commented bymr W last updated on 08/Mar/21
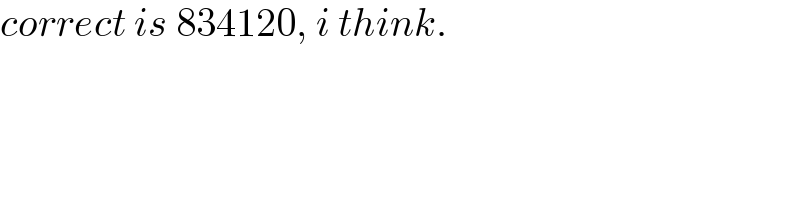
$${correct}\:{is}\:\mathrm{834120},\:{i}\:{think}. \\ $$
Commented bymath55 last updated on 08/Mar/21
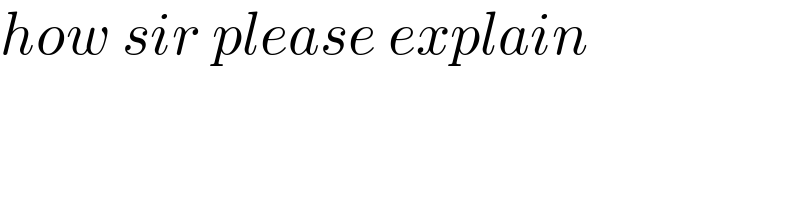
$${how}\:{sir}\:{please}\:{explain} \\ $$
Answered by mr W last updated on 08/Mar/21

$${to}\:{distribute}\:{n}\:{\color{mathblue}{i}\color{mathblue}{d}\color{mathblue}{e}\color{mathblue}{n}\color{mathblue}{t}\color{mathblue}{i}\color{mathblue}{c}\color{mathblue}{a}\color{mathblue}{l}}\:{objects} \\ $$ $${among}\:{r}\:{persions},\:{the}\:{number}\:{of} \\ $$ $${ways}\:{is}\:{the}\:{coefficient}\:{of}\:{x}^{{n}} \:{term}\:{in} \\ $$ $$\left({x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +...\right)^{{r}} \\ $$ $$\left({each}\:{person}\:{gets}\:{at}\:{least}\:{one}\:{object}\right) \\ $$ $$ \\ $$ $${if}\:{the}\:{n}\:{objects}\:{are}\color{mathblue}{\:}{\color{mathblue}{d}\color{mathblue}{i}\color{mathblue}{f}\color{mathblue}{f}\color{mathblue}{e}\color{mathblue}{r}\color{mathblue}{e}\color{mathblue}{n}\color{mathblue}{t}}, \\ $$ $${similarly}\:{the}\:{number}\:{of}\:{ways}\:{is}\:{the} \\ $$ $${coefficient}\:{of}\:{x}^{{n}} \:{term}\:{in} \\ $$ $${n}!\left({x}+\frac{\mathrm{1}}{\mathrm{2}!}{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{3}!}{x}^{\mathrm{3}} +...\right)^{{r}} ={n}!\left({e}^{{x}} −\mathrm{1}\right)^{{r}} \\ $$ $$ \\ $$ $${with}\:{n}=\mathrm{9},\:{r}=\mathrm{5}\:{we}\:{get}\:{the}\:{coef}.\:{of} \\ $$ $${x}^{\mathrm{9}} \:{in}\:\mathrm{9}!\left({e}^{{x}} −\mathrm{1}\right)^{\mathrm{5}} \:{is}\:\mathrm{\color{mathred}{8}\color{mathred}{3}\color{mathred}{4}\color{mathred}{1}\color{mathred}{2}\color{mathred}{0}}. \\ $$
Commented bymr W last updated on 08/Mar/21