Question and Answers Forum

All Question   Topic List

Question Number 134817 by bramlexs22 last updated on 07/Mar/21

$$ \\ $$ What is the maximum value of abc if a+b+c = 5 and ab+bc+ca = 7?\\n

Commented bybramlexs22 last updated on 09/Mar/21

thanks you all sir

$$\mathrm{thanks}\:\mathrm{you}\:\mathrm{all}\:\mathrm{sir} \\ $$

Commented byjohn_santu last updated on 08/Mar/21

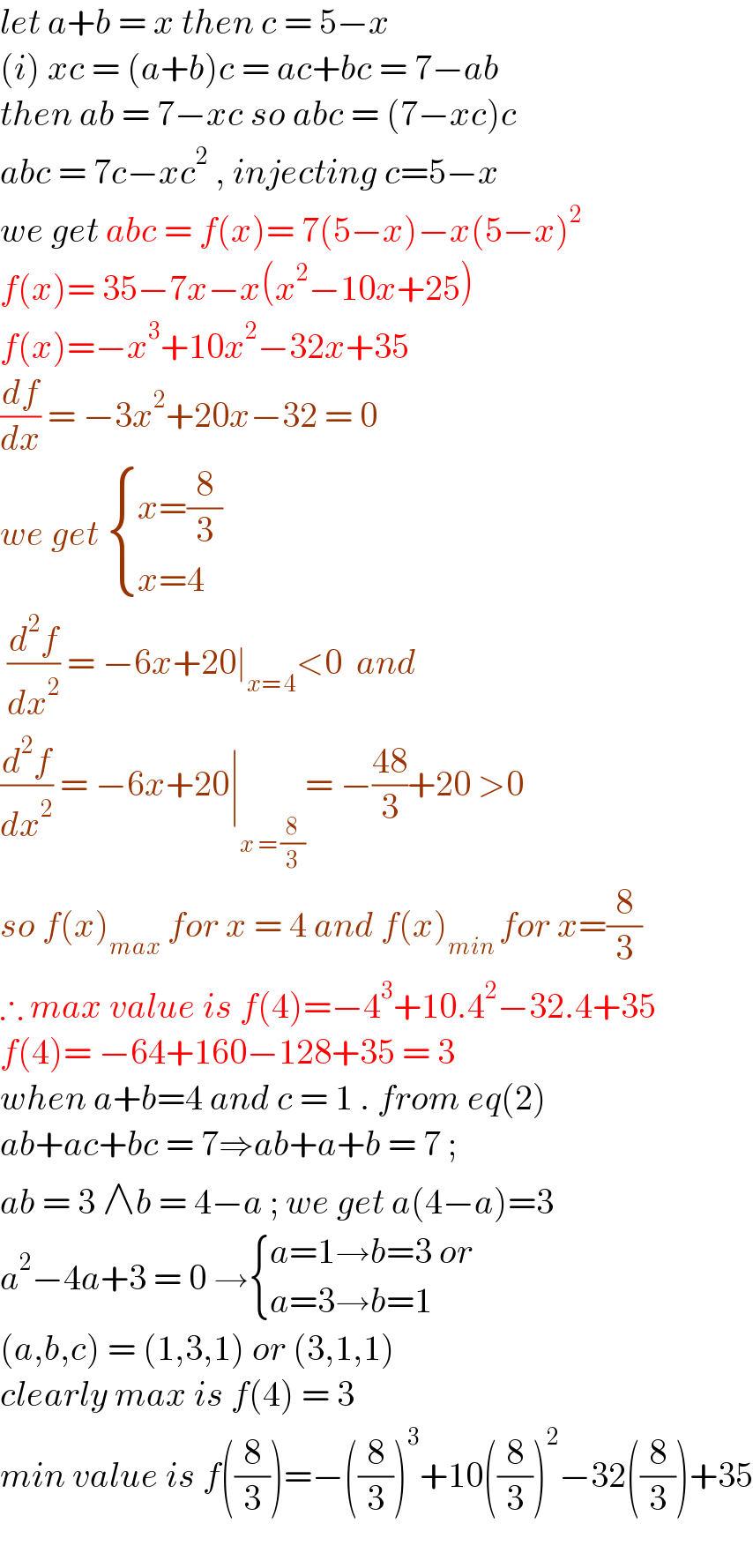
let a+b = x then c = 5−x (i) xc = (a+b)c = ac+bc = 7−ab then ab = 7−xc so abc = (7−xc)c abc = 7c−xc^2 , injecting c=5−x we get abc = f(x)= 7(5−x)−x(5−x)^2 f(x)= 35−7x−x(x^2 −10x+25) f(x)=−x^3 +10x^2 −32x+35 (df/dx) = −3x^2 +20x−32 = 0 we get { ((x=(8/3))),((x=4)) :} (d^2 f/dx^2 ) = −6x+20∣_(x= 4) <0 and (d^2 f/dx^2 ) = −6x+20∣_(x = (8/3)) = −((48)/3)+20 >0 so f(x)_(max) for x = 4 and f(x)_(min ) for x=(8/3) ∴ max value is f(4)=−4^3 +10.4^2 −32.4+35 f(4)= −64+160−128+35 = 3 when a+b=4 and c = 1 . from eq(2) ab+ac+bc = 7⇒ab+a+b = 7 ; ab = 3 ∧b = 4−a ; we get a(4−a)=3 a^2 −4a+3 = 0 → { ((a=1→b=3 or)),((a=3→b=1 )) :} (a,b,c) = (1,3,1) or (3,1,1) clearly max is f(4) = 3 min value is f((8/3))=−((8/3))^3 +10((8/3))^2 −32((8/3))+35

$${let}\:{a}+{b}\:=\:{x}\:{then}\:{c}\:=\:\mathrm{5}−{x} \\ $$ $$\left({i}\right)\:{xc}\:=\:\left({a}+{b}\right){c}\:=\:{ac}+{bc}\:=\:\mathrm{7}−{ab} \\ $$ $${then}\:{ab}\:=\:\mathrm{7}−{xc}\:{so}\:{abc}\:=\:\left(\mathrm{7}−{xc}\right){c} \\ $$ $${abc}\:=\:\mathrm{7}{c}−{xc}^{\mathrm{2}} \:,\:{injecting}\:{c}=\mathrm{5}−{x} \\ $$ $${we}\:{get}\:{\color{mathred}{a}\color{mathred}{b}\color{mathred}{c}}\color{mathred}{\:}\color{mathred}{=}\color{mathred}{\:}{\color{mathred}{f}}\color{mathred}{\left(}{\color{mathred}{x}}\color{mathred}{\right)}\color{mathred}{=}\color{mathred}{\:}\mathrm{\color{mathred}{7}}\color{mathred}{\left(}\mathrm{\color{mathred}{5}}\color{mathred}{−}{\color{mathred}{x}}\color{mathred}{\right)}\color{mathred}{−}{\color{mathred}{x}}\color{mathred}{\left(}\mathrm{\color{mathred}{5}}\color{mathred}{−}{\color{mathred}{x}}\color{mathred}{\right)}^{\mathrm{\color{mathred}{2}}} \\ $$ $${\color{mathred}{f}}\color{mathred}{\left(}{\color{mathred}{x}}\color{mathred}{\right)}\color{mathred}{=}\color{mathred}{\:}\mathrm{\color{mathred}{3}\color{mathred}{5}}\color{mathred}{−}\mathrm{\color{mathred}{7}}{\color{mathred}{x}}\color{mathred}{−}{\color{mathred}{x}}\color{mathred}{\left(}{\color{mathred}{x}}^{\mathrm{\color{mathred}{2}}} \color{mathred}{−}\mathrm{\color{mathred}{1}\color{mathred}{0}}{\color{mathred}{x}}\color{mathred}{+}\mathrm{\color{mathred}{2}\color{mathred}{5}}\color{mathred}{\right)} \\ $$ $${\color{mathred}{f}}\color{mathred}{\left(}{\color{mathred}{x}}\color{mathred}{\right)}\color{mathred}{=}\color{mathred}{−}{\color{mathred}{x}}^{\mathrm{\color{mathred}{3}}} \color{mathred}{+}\mathrm{\color{mathred}{1}\color{mathred}{0}}{\color{mathred}{x}}^{\mathrm{\color{mathred}{2}}} \color{mathred}{−}\mathrm{\color{mathred}{3}\color{mathred}{2}}{\color{mathred}{x}}\color{mathred}{+}\mathrm{\color{mathred}{3}\color{mathred}{5}}\color{mathred}{\:} \\ $$ $$\frac{{\color{mathbrown}{d}\color{mathbrown}{f}}}{{\color{mathbrown}{d}\color{mathbrown}{x}}}\color{mathbrown}{\:}\color{mathbrown}{=}\color{mathbrown}{\:}\color{mathbrown}{−}\mathrm{\color{mathbrown}{3}}{\color{mathbrown}{x}}^{\mathrm{\color{mathbrown}{2}}} \color{mathbrown}{+}\mathrm{\color{mathbrown}{2}\color{mathbrown}{0}}{\color{mathbrown}{x}}\color{mathbrown}{−}\mathrm{\color{mathbrown}{3}\color{mathbrown}{2}}\color{mathbrown}{\:}\color{mathbrown}{=}\color{mathbrown}{\:}\mathrm{\color{mathbrown}{0}} \\ $$ $${\color{mathbrown}{w}\color{mathbrown}{e}}\color{mathbrown}{\:}{\color{mathbrown}{g}\color{mathbrown}{e}\color{mathbrown}{t}}\color{mathbrown}{\:}\begin{cases}{{\color{mathbrown}{x}}\color{mathbrown}{=}\frac{\mathrm{\color{mathbrown}{8}}}{\mathrm{\color{mathbrown}{3}}}}\\{{\color{mathbrown}{x}}\color{mathbrown}{=}\mathrm{\color{mathbrown}{4}}}\end{cases} \\ $$ $$\color{mathbrown}{\:}\frac{{\color{mathbrown}{d}}^{\mathrm{\color{mathbrown}{2}}} {\color{mathbrown}{f}}}{{\color{mathbrown}{d}\color{mathbrown}{x}}^{\mathrm{\color{mathbrown}{2}}} }\color{mathbrown}{\:}\color{mathbrown}{=}\color{mathbrown}{\:}\color{mathbrown}{−}\mathrm{\color{mathbrown}{6}}{\color{mathbrown}{x}}\color{mathbrown}{+}\mathrm{\color{mathbrown}{2}\color{mathbrown}{0}}\color{mathbrown}{\mid}_{{\color{mathbrown}{x}}\color{mathbrown}{=}\color{mathbrown}{\:}\mathrm{\color{mathbrown}{4}}} \color{mathbrown}{<}\mathrm{\color{mathbrown}{0}}\color{mathbrown}{\:}\color{mathbrown}{\:}{\color{mathbrown}{a}\color{mathbrown}{n}\color{mathbrown}{d}}\color{mathbrown}{\:} \\ $$ $$\frac{{\color{mathbrown}{d}}^{\mathrm{\color{mathbrown}{2}}} {\color{mathbrown}{f}}}{{\color{mathbrown}{d}\color{mathbrown}{x}}^{\mathrm{\color{mathbrown}{2}}} }\color{mathbrown}{\:}\color{mathbrown}{=}\color{mathbrown}{\:}\color{mathbrown}{−}\mathrm{\color{mathbrown}{6}}{\color{mathbrown}{x}}\color{mathbrown}{+}\mathrm{\color{mathbrown}{2}\color{mathbrown}{0}}\color{mathbrown}{\mid}_{{\color{mathbrown}{x}}\color{mathbrown}{\:}\color{mathbrown}{=}\color{mathbrown}{\:}\frac{\mathrm{\color{mathbrown}{8}}}{\mathrm{\color{mathbrown}{3}}}} \color{mathbrown}{=}\color{mathbrown}{\:}\color{mathbrown}{−}\frac{\mathrm{\color{mathbrown}{4}\color{mathbrown}{8}}}{\mathrm{\color{mathbrown}{3}}}\color{mathbrown}{+}\mathrm{\color{mathbrown}{2}\color{mathbrown}{0}}\color{mathbrown}{\:}\color{mathbrown}{>}\mathrm{\color{mathbrown}{0}}\color{mathbrown}{\:} \\ $$ $${\color{mathbrown}{s}\color{mathbrown}{o}}\color{mathbrown}{\:}{\color{mathbrown}{f}}\color{mathbrown}{\left(}{\color{mathbrown}{x}}\color{mathbrown}{\right)}_{{\color{mathbrown}{m}\color{mathbrown}{a}\color{mathbrown}{x}}} \color{mathbrown}{\:}{\color{mathbrown}{f}\color{mathbrown}{o}\color{mathbrown}{r}}\color{mathbrown}{\:}{\color{mathbrown}{x}}\color{mathbrown}{\:}\color{mathbrown}{=}\color{mathbrown}{\:}\mathrm{\color{mathbrown}{4}}\color{mathbrown}{\:}{\color{mathbrown}{a}\color{mathbrown}{n}\color{mathbrown}{d}}\color{mathbrown}{\:}{\color{mathbrown}{f}}\color{mathbrown}{\left(}{\color{mathbrown}{x}}\color{mathbrown}{\right)}_{{\color{mathbrown}{m}\color{mathbrown}{i}\color{mathbrown}{n}}\color{mathbrown}{\:}} {\color{mathbrown}{f}\color{mathbrown}{o}\color{mathbrown}{r}}\color{mathbrown}{\:}{\color{mathbrown}{x}}\color{mathbrown}{=}\frac{\mathrm{\color{mathbrown}{8}}}{\mathrm{\color{mathbrown}{3}}} \\ $$ $$\color{mathred}{\therefore}\color{mathred}{\:}{\color{mathred}{m}\color{mathred}{a}\color{mathred}{x}}\color{mathred}{\:}{\color{mathred}{v}\color{mathred}{a}\color{mathred}{l}\color{mathred}{u}\color{mathred}{e}}\color{mathred}{\:}{\color{mathred}{i}\color{mathred}{s}}\color{mathred}{\:}{\color{mathred}{f}}\color{mathred}{\left(}\mathrm{\color{mathred}{4}}\color{mathred}{\right)}\color{mathred}{=}\color{mathred}{−}\mathrm{\color{mathred}{4}}^{\mathrm{\color{mathred}{3}}} \color{mathred}{+}\mathrm{\color{mathred}{1}\color{mathred}{0}}\color{mathred}{.}\mathrm{\color{mathred}{4}}^{\mathrm{\color{mathred}{2}}} \color{mathred}{−}\mathrm{\color{mathred}{3}\color{mathred}{2}}\color{mathred}{.}\mathrm{\color{mathred}{4}}\color{mathred}{+}\mathrm{\color{mathred}{3}\color{mathred}{5}}\color{mathred}{\:} \\ $$ $${\color{mathred}{f}}\color{mathred}{\left(}\mathrm{\color{mathred}{4}}\color{mathred}{\right)}\color{mathred}{=}\color{mathred}{\:}\color{mathred}{−}\mathrm{\color{mathred}{6}\color{mathred}{4}}\color{mathred}{+}\mathrm{\color{mathred}{1}\color{mathred}{6}\color{mathred}{0}}\color{mathred}{−}\mathrm{\color{mathred}{1}\color{mathred}{2}\color{mathred}{8}}\color{mathred}{+}\mathrm{\color{mathred}{3}\color{mathred}{5}}\color{mathred}{\:}\color{mathred}{=}\color{mathred}{\:}\mathrm{\color{mathred}{3}} \\ $$ $${when}\:{a}+{b}=\mathrm{4}\:{and}\:{c}\:=\:\mathrm{1}\:.\:{from}\:{eq}\left(\mathrm{2}\right) \\ $$ $${ab}+{ac}+{bc}\:=\:\mathrm{7}\Rightarrow{ab}+{a}+{b}\:=\:\mathrm{7}\:;\: \\ $$ $${ab}\:=\:\mathrm{3}\:\wedge{b}\:=\:\mathrm{4}−{a}\:;\:{we}\:{get}\:{a}\left(\mathrm{4}−{a}\right)=\mathrm{3} \\ $$ $${a}^{\mathrm{2}} −\mathrm{4}{a}+\mathrm{3}\:=\:\mathrm{0}\:\rightarrow\begin{cases}{{a}=\mathrm{1}\rightarrow{b}=\mathrm{3}\:{or}}\\{{a}=\mathrm{3}\rightarrow{b}=\mathrm{1}\:}\end{cases} \\ $$ $$\left({a},{b},{c}\right)\:=\:\left(\mathrm{1},\mathrm{3},\mathrm{1}\right)\:{or}\:\left(\mathrm{3},\mathrm{1},\mathrm{1}\right) \\ $$ $${clearly}\:{max}\:{is}\:{f}\left(\mathrm{4}\right)\:=\:\mathrm{3} \\ $$ $${min}\:{value}\:{is}\:{f}\left(\frac{\mathrm{8}}{\mathrm{3}}\right)=−\left(\frac{\mathrm{8}}{\mathrm{3}}\right)^{\mathrm{3}} +\mathrm{10}\left(\frac{\mathrm{8}}{\mathrm{3}}\right)^{\mathrm{2}} −\mathrm{32}\left(\frac{\mathrm{8}}{\mathrm{3}}\right)+\mathrm{35} \\ $$ $$ \\ $$

Commented bymr W last updated on 08/Mar/21

very nice! i used also similar method, but maybe made a calculation mistake somewhere.

$${very}\:{nice}!\:{i}\:{used}\:{also}\:{similar}\:{method},\: \\ $$ $${but}\:{maybe}\:{made}\:{a}\:{calculation}\:{mistake} \\ $$ $${somewhere}. \\ $$

Answered by liberty last updated on 07/Mar/21

(1)a=5−(b+c) (2) (5−(b+c))b+bc+c(5−(b+c))=7 ⇒ 5b−b^2 −bc+bc+5c−bc−c^2 =7 ⇒5b−b^2 −bc+5c+c^2 = 7 (3)abc = (5−(b+c))bc =5bc−b^2 c−bc^2 let f(b,c)=5bc−b^2 c−bc^2 +λ(5b−b^2 −bc+5c+c^2 −7) (i) f_b = 5c−2bc−c^2 +λ(5−2b−c)=0 (ii)f_c = 5b−b^2 −2bc+λ(−b+5+2c)= 0 (iii)f_(λ ) = 5b−b^2 −bc+5c+c^2 = 7 from eq (i) &(ii) we get { ((λ=((c^2 +2bc−5c)/(5−2b−c)))),((λ = ((b^2 +2bc−5b)/(5−b+2c)))) :} and b^2 −5b = c^2 +5c−bc−7 ⇒ λ = λ ; ((c^2 +2bc−5c)/(5−2b−c)) = ((c^2 +5c−bc−7+2bc)/(5−b+2c)) next...

$$\left(\mathrm{1}\right){a}=\mathrm{5}−\left({b}+{c}\right)\:\left(\mathrm{2}\right)\:\left(\mathrm{5}−\left({b}+{c}\right)\right){b}+{bc}+{c}\left(\mathrm{5}−\left({b}+{c}\right)\right)=\mathrm{7} \\ $$ $$\Rightarrow\:\mathrm{5}{b}−{b}^{\mathrm{2}} −{bc}+{bc}+\mathrm{5}{c}−{bc}−{c}^{\mathrm{2}} =\mathrm{7} \\ $$ $$\Rightarrow\mathrm{5}{b}−{b}^{\mathrm{2}} −{bc}+\mathrm{5}{c}+{c}^{\mathrm{2}} \:=\:\mathrm{7} \\ $$ $$\left(\mathrm{3}\right){abc}\:=\:\left(\mathrm{5}−\left({b}+{c}\right)\right){bc}\:=\mathrm{5}{bc}−{b}^{\mathrm{2}} {c}−{bc}^{\mathrm{2}} \\ $$ $${let}\:{f}\left({b},{c}\right)=\mathrm{5}{bc}−{b}^{\mathrm{2}} {c}−{bc}^{\mathrm{2}} +\lambda\left(\mathrm{5}{b}−{b}^{\mathrm{2}} −{bc}+\mathrm{5}{c}+{c}^{\mathrm{2}} −\mathrm{7}\right) \\ $$ $$\color{mathblue}{\left(}{\color{mathblue}{i}}\color{mathblue}{\right)}\color{mathblue}{\:}{\color{mathblue}{f}}_{{\color{mathblue}{b}}} \color{mathblue}{=}\color{mathblue}{\:}\mathrm{\color{mathblue}{5}}{\color{mathblue}{c}}\color{mathblue}{−}\mathrm{\color{mathblue}{2}}{\color{mathblue}{b}\color{mathblue}{c}}\color{mathblue}{−}{\color{mathblue}{c}}^{\mathrm{\color{mathblue}{2}}} \color{mathblue}{+}\color{mathblue}{\lambda}\color{mathblue}{\left(}\mathrm{\color{mathblue}{5}}\color{mathblue}{−}\mathrm{\color{mathblue}{2}}{\color{mathblue}{b}}\color{mathblue}{−}{\color{mathblue}{c}}\color{mathblue}{\right)}\color{mathblue}{=}\mathrm{\color{mathblue}{0}} \\ $$ $$\color{mathblue}{\left(}{\color{mathblue}{i}\color{mathblue}{i}}\color{mathblue}{\right)}{\color{mathblue}{f}}_{{\color{mathblue}{c}}} \color{mathblue}{=}\color{mathblue}{\:}\mathrm{\color{mathblue}{5}}{\color{mathblue}{b}}\color{mathblue}{−}{\color{mathblue}{b}}^{\mathrm{\color{mathblue}{2}}} \color{mathblue}{−}\mathrm{\color{mathblue}{2}}{\color{mathblue}{b}\color{mathblue}{c}}\color{mathblue}{+}\color{mathblue}{\lambda}\color{mathblue}{\left(}\color{mathblue}{−}{\color{mathblue}{b}}\color{mathblue}{+}\mathrm{\color{mathblue}{5}}\color{mathblue}{+}\mathrm{\color{mathblue}{2}}{\color{mathblue}{c}}\color{mathblue}{\right)}\color{mathblue}{=}\color{mathblue}{\:}\mathrm{\color{mathblue}{0}} \\ $$ $$\color{mathblue}{\left(}{\color{mathblue}{i}\color{mathblue}{i}\color{mathblue}{i}}\color{mathblue}{\right)}{\color{mathblue}{f}}_{\color{mathblue}{\lambda}\color{mathblue}{\:}} \color{mathblue}{=}\color{mathblue}{\:}\mathrm{\color{mathblue}{5}}{\color{mathblue}{b}}\color{mathblue}{−}{\color{mathblue}{b}}^{\mathrm{\color{mathblue}{2}}} \color{mathblue}{−}{\color{mathblue}{b}\color{mathblue}{c}}\color{mathblue}{+}\mathrm{\color{mathblue}{5}}{\color{mathblue}{c}}\color{mathblue}{+}{\color{mathblue}{c}}^{\mathrm{\color{mathblue}{2}}} \color{mathblue}{\:}\color{mathblue}{=}\color{mathblue}{\:}\mathrm{\color{mathblue}{7}} \\ $$ $${\color{mathbrown}{f}\color{mathbrown}{r}\color{mathbrown}{o}\color{mathbrown}{m}}\color{mathbrown}{\:}{\color{mathbrown}{e}\color{mathbrown}{q}}\color{mathbrown}{\:}\color{mathbrown}{\left(}{\color{mathbrown}{i}}\color{mathbrown}{\right)}\color{mathbrown}{\:}\&\color{mathbrown}{\left(}{\color{mathbrown}{i}\color{mathbrown}{i}}\color{mathbrown}{\right)}\color{mathbrown}{\:}{\color{mathbrown}{w}\color{mathbrown}{e}}\color{mathbrown}{\:}{\color{mathbrown}{g}\color{mathbrown}{e}\color{mathbrown}{t}}\color{mathbrown}{\:}\begin{cases}{\color{mathbrown}{\lambda}\color{mathbrown}{=}\frac{{\color{mathbrown}{c}}^{\mathrm{\color{mathbrown}{2}}} \color{mathbrown}{+}\mathrm{\color{mathbrown}{2}}{\color{mathbrown}{b}\color{mathbrown}{c}}\color{mathbrown}{−}\mathrm{\color{mathbrown}{5}}{\color{mathbrown}{c}}}{\mathrm{\color{mathbrown}{5}}\color{mathbrown}{−}\mathrm{\color{mathbrown}{2}}{\color{mathbrown}{b}}\color{mathbrown}{−}{\color{mathbrown}{c}}}}\\{\color{mathbrown}{\lambda}\color{mathbrown}{\:}\color{mathbrown}{=}\color{mathbrown}{\:}\frac{{\color{mathbrown}{b}}^{\mathrm{\color{mathbrown}{2}}} \color{mathbrown}{+}\mathrm{\color{mathbrown}{2}}{\color{mathbrown}{b}\color{mathbrown}{c}}\color{mathbrown}{−}\mathrm{\color{mathbrown}{5}}{\color{mathbrown}{b}}}{\mathrm{\color{mathbrown}{5}}\color{mathbrown}{−}{\color{mathbrown}{b}}\color{mathbrown}{+}\mathrm{\color{mathbrown}{2}}{\color{mathbrown}{c}}}}\end{cases} \\ $$ $${\color{mathbrown}{a}\color{mathbrown}{n}\color{mathbrown}{d}}\color{mathbrown}{\:}{\color{mathbrown}{b}}^{\mathrm{\color{mathbrown}{2}}} \color{mathbrown}{−}\mathrm{\color{mathbrown}{5}}{\color{mathbrown}{b}}\color{mathbrown}{\:}\color{mathbrown}{=}\color{mathbrown}{\:}{\color{mathbrown}{c}}^{\mathrm{\color{mathbrown}{2}}} \color{mathbrown}{+}\mathrm{\color{mathbrown}{5}}{\color{mathbrown}{c}}\color{mathbrown}{−}{\color{mathbrown}{b}\color{mathbrown}{c}}\color{mathbrown}{−}\mathrm{\color{mathbrown}{7}} \\ $$ $$\color{mathred}{\Rightarrow}\color{mathred}{\:}\color{mathred}{\lambda}\color{mathred}{\:}\color{mathred}{=}\color{mathred}{\:}\color{mathred}{\lambda}\color{mathred}{\:}\color{mathred}{;}\color{mathred}{\:}\frac{{\color{mathred}{c}}^{\mathrm{\color{mathred}{2}}} \color{mathred}{+}\mathrm{\color{mathred}{2}}{\color{mathred}{b}\color{mathred}{c}}\color{mathred}{−}\mathrm{\color{mathred}{5}}{\color{mathred}{c}}}{\mathrm{\color{mathred}{5}}\color{mathred}{−}\mathrm{\color{mathred}{2}}{\color{mathred}{b}}\color{mathred}{−}{\color{mathred}{c}}}\color{mathred}{\:}\color{mathred}{=}\color{mathred}{\:}\frac{{\color{mathred}{c}}^{\mathrm{\color{mathred}{2}}} \color{mathred}{+}\mathrm{\color{mathred}{5}}{\color{mathred}{c}}\color{mathred}{−}{\color{mathred}{b}\color{mathred}{c}}\color{mathred}{−}\mathrm{\color{mathred}{7}}\color{mathred}{+}\mathrm{\color{mathred}{2}}{\color{mathred}{b}\color{mathred}{c}}}{\mathrm{\color{mathred}{5}}\color{mathred}{−}{\color{mathred}{b}}\color{mathred}{+}\mathrm{\color{mathred}{2}}{\color{mathred}{c}}} \\ $$ $${\color{mathred}{n}\color{mathred}{e}\color{mathred}{x}\color{mathred}{t}}\color{mathred}{.}\color{mathred}{.}\color{mathred}{.} \\ $$

Answered by mr W last updated on 08/Mar/21

c=5−(a+b) ab+(a+b)c=7 c=((7−ab)/(a+b))=5−(a+b) ⇒ab=7−(a+b)(5−(a+b)) P=abc=ab(5−(a+b))=[7−(a+b)(5−(a+b))](5−(a+b)) let t=a+b ⇒P=[7−t(5−t)](5−t)=−t^3 +10t^2 −32t+35 (dP/dt)=−3t^2 +20t−32=0 (3t−8)(t−4)=0 ⇒t=(8/3), 4 (d^2 P/dt^2 )=−6t+20 at t=(8/3): (d^2 P/dt^2 )=−6×(8/3)+20=4>0 ⇒min. at t=4: (d^2 P/dt^2 )=−6×4+20=−4<0 ⇒max. ⇒P_(min) =[7−(8/3)(5−(8/3))](5−(8/3))=((49)/(27)) ⇒P_(max) =[7−4(5−4)](5−4)=3

$${c}=\mathrm{5}−\left({a}+{b}\right) \\ $$ $${ab}+\left({a}+{b}\right){c}=\mathrm{7} \\ $$ $${c}=\frac{\mathrm{7}−{ab}}{{a}+{b}}=\mathrm{5}−\left({a}+{b}\right) \\ $$ $$\Rightarrow{ab}=\mathrm{7}−\left({a}+{b}\right)\left(\mathrm{5}−\left({a}+{b}\right)\right) \\ $$ $${P}={abc}={ab}\left(\mathrm{5}−\left({a}+{b}\right)\right)=\left[\mathrm{7}−\left({a}+{b}\right)\left(\mathrm{5}−\left({a}+{b}\right)\right)\right]\left(\mathrm{5}−\left({a}+{b}\right)\right) \\ $$ $${let}\:{t}={a}+{b} \\ $$ $$\Rightarrow{P}=\left[\mathrm{7}−{t}\left(\mathrm{5}−{t}\right)\right]\left(\mathrm{5}−{t}\right)=−{t}^{\mathrm{3}} +\mathrm{10}{t}^{\mathrm{2}} −\mathrm{32}{t}+\mathrm{35} \\ $$ $$\frac{{dP}}{{dt}}=−\mathrm{3}{t}^{\mathrm{2}} +\mathrm{20}{t}−\mathrm{32}=\mathrm{0} \\ $$ $$\left(\mathrm{3}{t}−\mathrm{8}\right)\left({t}−\mathrm{4}\right)=\mathrm{0} \\ $$ $$\Rightarrow{t}=\frac{\mathrm{8}}{\mathrm{3}},\:\mathrm{4} \\ $$ $$\frac{{d}^{\mathrm{2}} {P}}{{dt}^{\mathrm{2}} }=−\mathrm{6}{t}+\mathrm{20} \\ $$ $${at}\:{t}=\frac{\mathrm{8}}{\mathrm{3}}:\:\frac{{d}^{\mathrm{2}} {P}}{{dt}^{\mathrm{2}} }=−\mathrm{6}×\frac{\mathrm{8}}{\mathrm{3}}+\mathrm{20}=\mathrm{4}>\mathrm{0}\:\Rightarrow{min}. \\ $$ $${at}\:{t}=\mathrm{4}:\:\frac{{d}^{\mathrm{2}} {P}}{{dt}^{\mathrm{2}} }=−\mathrm{6}×\mathrm{4}+\mathrm{20}=−\mathrm{4}<\mathrm{0}\:\Rightarrow{max}. \\ $$ $$\Rightarrow{P}_{{min}} =\left[\mathrm{7}−\frac{\mathrm{8}}{\mathrm{3}}\left(\mathrm{5}−\frac{\mathrm{8}}{\mathrm{3}}\right)\right]\left(\mathrm{5}−\frac{\mathrm{8}}{\mathrm{3}}\right)=\frac{\mathrm{49}}{\mathrm{27}} \\ $$ $$\Rightarrow{P}_{{max}} =\left[\mathrm{7}−\mathrm{4}\left(\mathrm{5}−\mathrm{4}\right)\right]\left(\mathrm{5}−\mathrm{4}\right)=\mathrm{3} \\ $$

Answered by ajfour last updated on 08/Mar/21

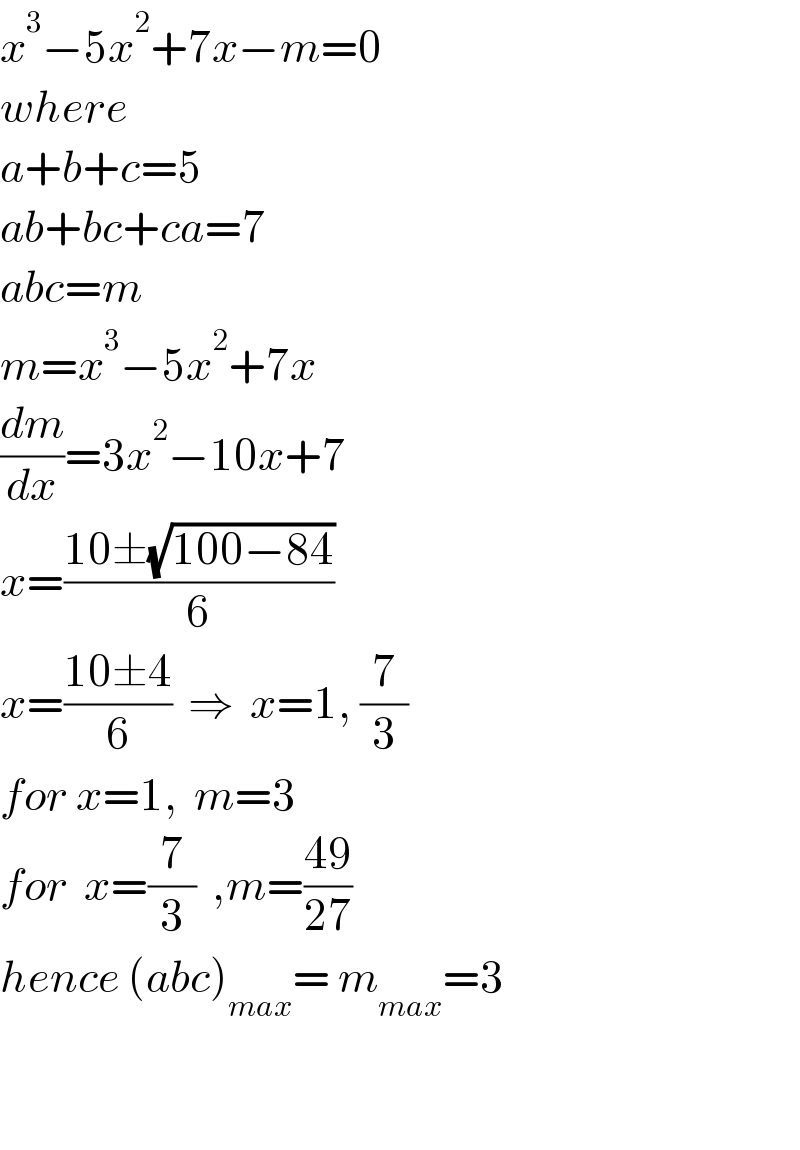
x^3 −5x^2 +7x−m=0 where a+b+c=5 ab+bc+ca=7 abc=m m=x^3 −5x^2 +7x (dm/dx)=3x^2 −10x+7 x=((10±(√(100−84)))/6) x=((10±4)/6) ⇒ x=1, (7/3) for x=1, m=3 for x=(7/3) ,m=((49)/(27)) hence (abc)_(max) = m_(max) =3

$${x}^{\mathrm{3}} −\mathrm{5}{x}^{\mathrm{2}} +\mathrm{7}{x}−{m}=\mathrm{0} \\ $$ $${where} \\ $$ $${a}+{b}+{c}=\mathrm{5} \\ $$ $${ab}+{bc}+{ca}=\mathrm{7} \\ $$ $${abc}={m} \\ $$ $${m}={x}^{\mathrm{3}} −\mathrm{5}{x}^{\mathrm{2}} +\mathrm{7}{x} \\ $$ $$\frac{{dm}}{{dx}}=\mathrm{3}{x}^{\mathrm{2}} −\mathrm{10}{x}+\mathrm{7} \\ $$ $${x}=\frac{\mathrm{10}\pm\sqrt{\mathrm{100}−\mathrm{84}}}{\mathrm{6}} \\ $$ $${x}=\frac{\mathrm{10}\pm\mathrm{4}}{\mathrm{6}}\:\:\Rightarrow\:\:{x}=\mathrm{1},\:\frac{\mathrm{7}}{\mathrm{3}} \\ $$ $${for}\:{x}=\mathrm{1},\:\:{m}=\mathrm{3} \\ $$ $${for}\:\:{x}=\frac{\mathrm{7}}{\mathrm{3}}\:\:,{m}=\frac{\mathrm{49}}{\mathrm{27}} \\ $$ $${hence}\:\left({abc}\right)_{{max}} =\:{m}_{{max}} =\mathrm{3} \\ $$ $$ \\ $$ $$ \\ $$

Commented bymr W last updated on 09/Mar/21

nice idea!

$${nice}\:{idea}! \\ $$

Commented byajfour last updated on 09/Mar/21

thanks sir, m little shaken by circumstances, n anyway taken to watching Utube movies n music, cant focus here like i used to, lets see how long; I m so very unpredictable even to myself...

$${thanks}\:{sir},\:{m}\:{little}\:{shaken}\:{by} \\ $$ $${circumstances},\:{n}\:{anyway}\:{taken} \\ $$ $${to}\:{watching}\:{Utube}\:{movies}\:{n} \\ $$ $${music},\:{cant}\:{focus}\:{here}\:{like}\:{i} \\ $$ $${used}\:{to},\:{lets}\:{see}\:{how}\:{long};\:{I}\:{m} \\ $$ $${so}\:{very}\:{unpredictable}\:{even}\:{to} \\ $$ $${myself}... \\ $$

Commented bymr W last updated on 09/Mar/21

take best care of yourself sir!

$${take}\:{best}\:{care}\:{of}\:{yourself}\:{sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com