
Question Number 134811 by bramlexs22 last updated on 07/Mar/21
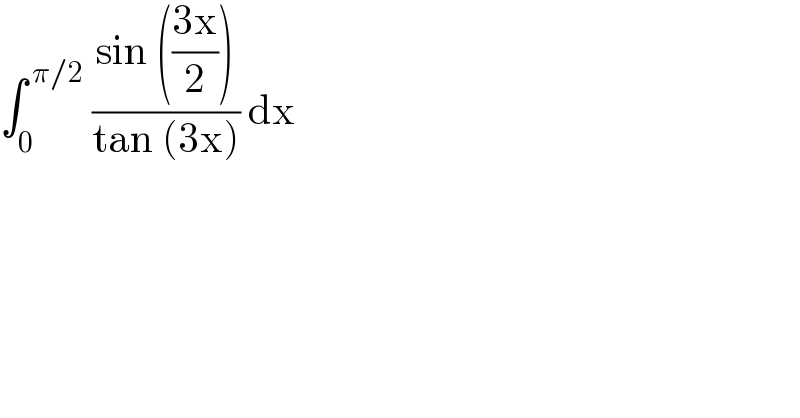
$$\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \:\frac{\mathrm{sin}\:\left(\frac{\mathrm{3x}}{\mathrm{2}}\right)}{\mathrm{tan}\:\left(\mathrm{3x}\right)}\:\mathrm{dx} \\ $$
Answered by EDWIN88 last updated on 07/Mar/21
![set ((3x)/2) = t ⇒ 3x = 2t , determinant (((x=(π/2)→t=((3π)/4))),((x=0 →t=0))) L = ∫_0 ^( 3π/4) ((sin t)/(tan 2t)) ((2/3)dt) L =(2/3)∫_0 ^( 3π/4) ((cos 2t sin t)/(2sin tcos t)) dt L = (1/3)∫_0 ^( 3π/4) ((cos 2t)/(cos t)) dt = (1/3)∫_0 ^( 3π/4) ((2cos^2 t−1)/(cos t)) dt L=(1/3)[ 2sin t−ln ∣sec t +tan t ∣ ]_0 ^((3π)/4) L=(1/3) [ (√2)−ln ∣(√2) +1∣ ]](Q134813.png)
$$\mathrm{set}\:\frac{\mathrm{3x}}{\mathrm{2}}\:=\:\mathrm{t}\:\Rightarrow\:\mathrm{3x}\:=\:\mathrm{2t}\:,\:\begin{array}{|c|c|}{\mathrm{x}=\frac{\pi}{\mathrm{2}}\rightarrow\mathrm{t}=\frac{\mathrm{3}\pi}{\mathrm{4}}}\\{\mathrm{x}=\mathrm{0}\:\rightarrow\mathrm{t}=\mathrm{0}}\\\hline\end{array} \\ $$$$\mathbb{L}\:=\:\int_{\mathrm{0}} ^{\:\mathrm{3}\pi/\mathrm{4}} \frac{\mathrm{sin}\:\mathrm{t}}{\mathrm{tan}\:\mathrm{2t}}\:\left(\frac{\mathrm{2}}{\mathrm{3}}\mathrm{dt}\right) \\ $$$$\mathbb{L}\:=\frac{\mathrm{2}}{\mathrm{3}}\int_{\mathrm{0}} ^{\:\mathrm{3}\pi/\mathrm{4}} \frac{\mathrm{cos}\:\mathrm{2t}\:\mathrm{sin}\:\mathrm{t}}{\mathrm{2sin}\:\mathrm{tcos}\:\mathrm{t}}\:\mathrm{dt}\: \\ $$$$\mathbb{L}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\:\mathrm{3}\pi/\mathrm{4}} \:\frac{\mathrm{cos}\:\mathrm{2}{t}}{\mathrm{cos}\:{t}}\:{dt}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\:\mathrm{3}\pi/\mathrm{4}} \:\frac{\mathrm{2cos}\:^{\mathrm{2}} \mathrm{t}−\mathrm{1}}{\mathrm{cos}\:\mathrm{t}}\:\mathrm{dt}\: \\ $$$$\mathbb{L}=\frac{\mathrm{1}}{\mathrm{3}}\left[\:\mathrm{2sin}\:\mathrm{t}−\mathrm{ln}\:\mid\mathrm{sec}\:\mathrm{t}\:+\mathrm{tan}\:\mathrm{t}\:\mid\:\right]_{\mathrm{0}} ^{\frac{\mathrm{3}\pi}{\mathrm{4}}} \\ $$$$\mathbb{L}=\frac{\mathrm{1}}{\mathrm{3}}\:\left[\:\sqrt{\mathrm{2}}−\mathrm{ln}\:\mid\sqrt{\mathrm{2}}\:+\mathrm{1}\mid\:\right]\: \\ $$
