
Question Number 120614 by TANMAY PANACEA last updated on 01/Nov/20
$${Trigonometry}\: \\ $$
Commented by TANMAY PANACEA last updated on 01/Nov/20

Commented by TANMAY PANACEA last updated on 01/Nov/20

Commented by TANMAY PANACEA last updated on 01/Nov/20

Commented by TANMAY PANACEA last updated on 01/Nov/20

Commented by Dwaipayan Shikari last updated on 01/Nov/20
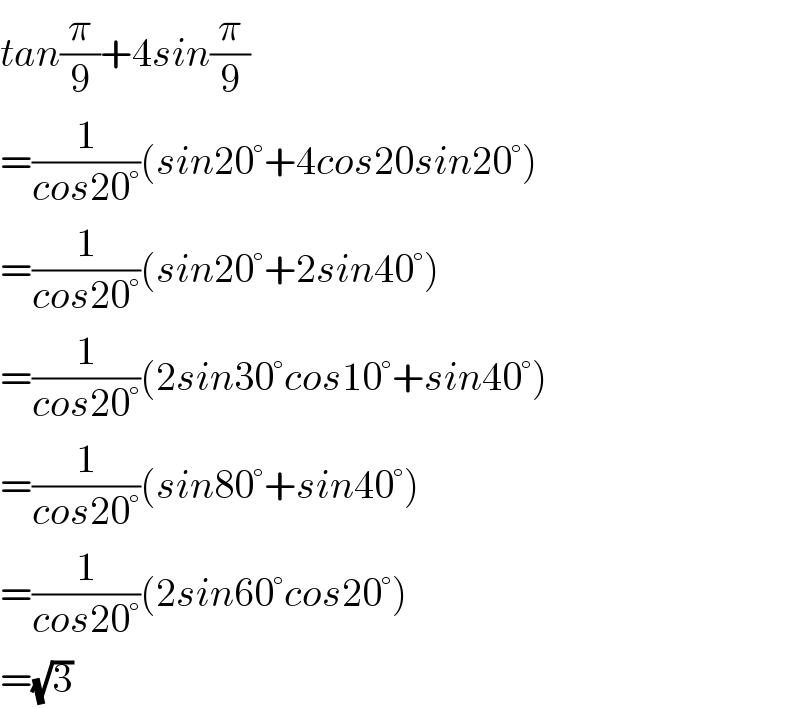
$${tan}\frac{\pi}{\mathrm{9}}+\mathrm{4}{sin}\frac{\pi}{\mathrm{9}} \\ $$$$=\frac{\mathrm{1}}{{cos}\mathrm{20}°}\left({sin}\mathrm{20}°+\mathrm{4}{cos}\mathrm{20}{sin}\mathrm{20}°\right) \\ $$$$=\frac{\mathrm{1}}{{cos}\mathrm{20}°}\left({sin}\mathrm{20}°+\mathrm{2}{sin}\mathrm{40}°\right) \\ $$$$=\frac{\mathrm{1}}{{cos}\mathrm{20}°}\left(\mathrm{2}{sin}\mathrm{30}°{cos}\mathrm{10}°+{sin}\mathrm{40}°\right) \\ $$$$=\frac{\mathrm{1}}{{cos}\mathrm{20}°}\left({sin}\mathrm{80}°+{sin}\mathrm{40}°\right) \\ $$$$=\frac{\mathrm{1}}{{cos}\mathrm{20}°}\left(\mathrm{2}{sin}\mathrm{60}°{cos}\mathrm{20}°\right) \\ $$$$=\sqrt{\mathrm{3}} \\ $$
Commented by Dwaipayan Shikari last updated on 01/Nov/20
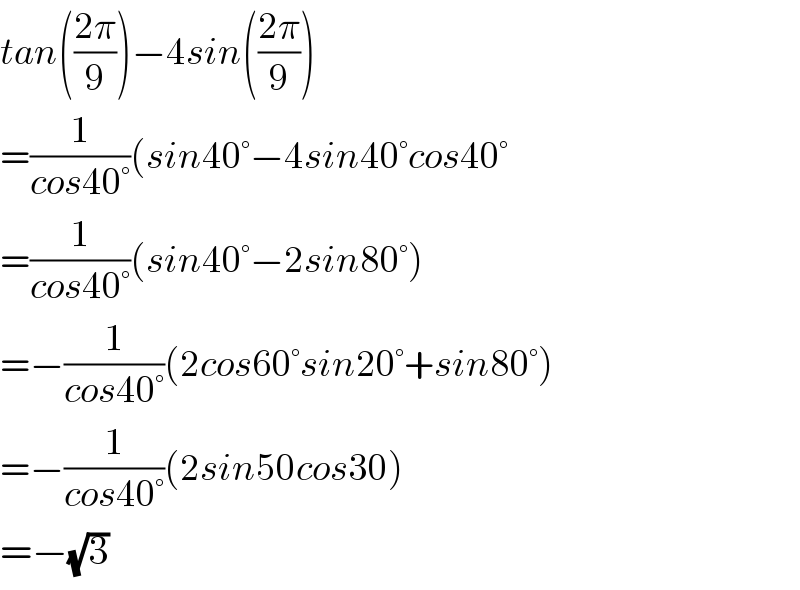
$${tan}\left(\frac{\mathrm{2}\pi}{\mathrm{9}}\right)−\mathrm{4}{sin}\left(\frac{\mathrm{2}\pi}{\mathrm{9}}\right) \\ $$$$=\frac{\mathrm{1}}{{cos}\mathrm{40}°}\left({sin}\mathrm{40}°−\mathrm{4}{sin}\mathrm{40}°{cos}\mathrm{40}°\right. \\ $$$$=\frac{\mathrm{1}}{{cos}\mathrm{40}°}\left({sin}\mathrm{40}°−\mathrm{2}{sin}\mathrm{80}°\right) \\ $$$$=−\frac{\mathrm{1}}{{cos}\mathrm{40}°}\left(\mathrm{2}{cos}\mathrm{60}°{sin}\mathrm{20}°+{sin}\mathrm{80}°\right) \\ $$$$=−\frac{\mathrm{1}}{{cos}\mathrm{40}°}\left(\mathrm{2}{sin}\mathrm{50}{cos}\mathrm{30}\right) \\ $$$$=−\sqrt{\mathrm{3}} \\ $$
Commented by TANMAY PANACEA last updated on 01/Nov/20

$${thank}\:{you} \\ $$
Commented by TANMAY PANACEA last updated on 01/Nov/20

$${thank}\:{you} \\ $$
