
Question Number 134601 by abdullahquwatan last updated on 05/Mar/21
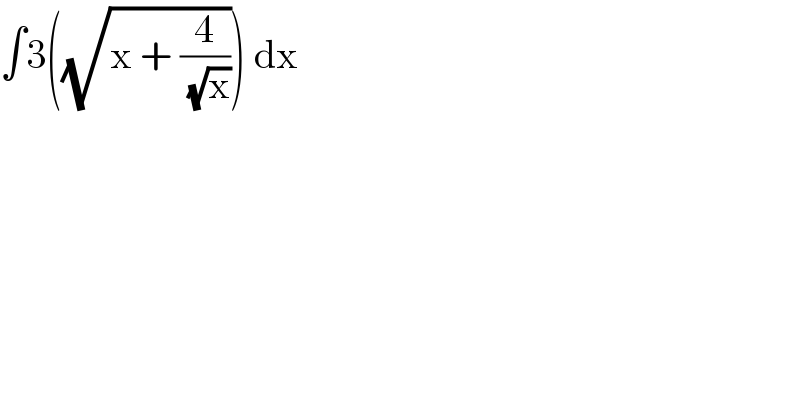
$$\int\mathrm{3}\left(\sqrt{\mathrm{x}\:+\:\frac{\mathrm{4}}{\:\sqrt{\mathrm{x}}}}\right)\:\mathrm{dx} \\ $$
Answered by bobhans last updated on 06/Mar/21
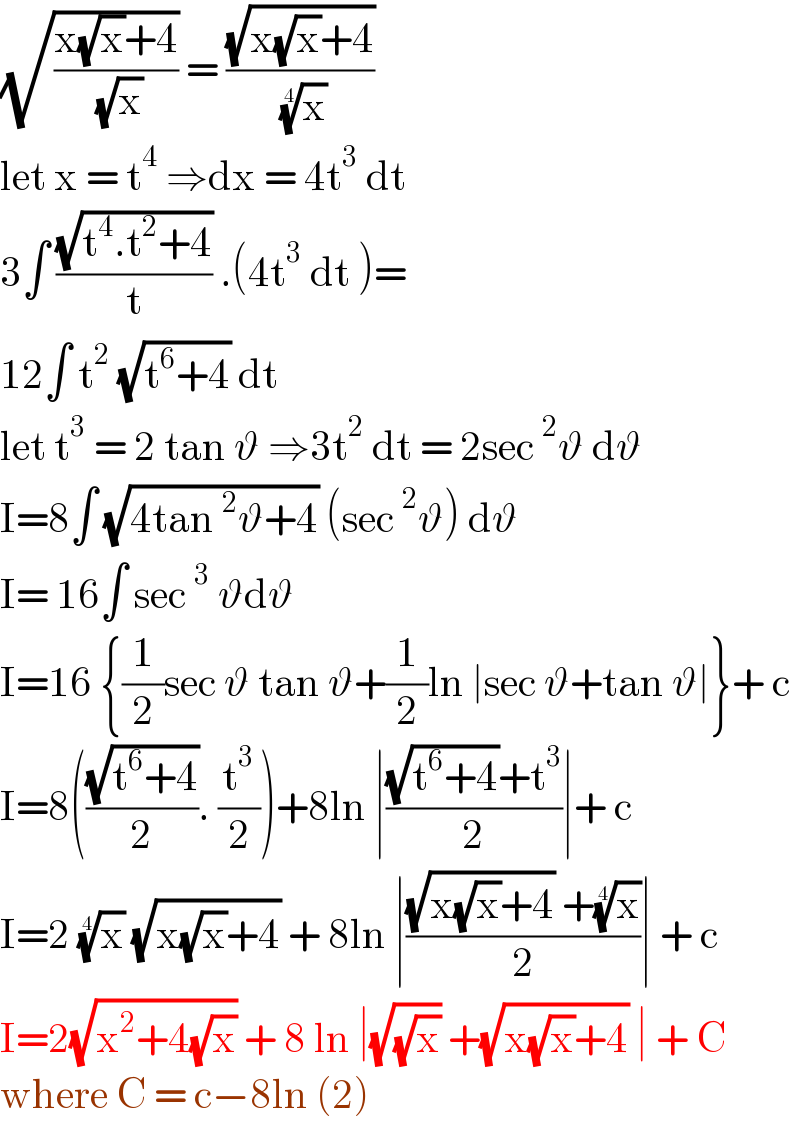
$$\sqrt{\frac{\mathrm{x}\sqrt{\mathrm{x}}+\mathrm{4}}{\:\sqrt{\mathrm{x}}}}\:=\:\frac{\sqrt{\mathrm{x}\sqrt{\mathrm{x}}+\mathrm{4}}}{\:\sqrt[{\mathrm{4}}]{\mathrm{x}}}\: \\ $$$$\mathrm{let}\:\mathrm{x}\:=\:\mathrm{t}^{\mathrm{4}} \:\Rightarrow\mathrm{dx}\:=\:\mathrm{4t}^{\mathrm{3}} \:\mathrm{dt} \\ $$$$\mathrm{3}\int\:\frac{\sqrt{\mathrm{t}^{\mathrm{4}} .\mathrm{t}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{t}}\:.\left(\mathrm{4t}^{\mathrm{3}} \:\mathrm{dt}\:\right)= \\ $$$$\mathrm{12}\int\:\mathrm{t}^{\mathrm{2}} \:\sqrt{\mathrm{t}^{\mathrm{6}} +\mathrm{4}}\:\mathrm{dt}\: \\ $$$$\mathrm{let}\:\mathrm{t}^{\mathrm{3}} \:=\:\mathrm{2}\:\mathrm{tan}\:\vartheta\:\Rightarrow\mathrm{3t}^{\mathrm{2}} \:\mathrm{dt}\:=\:\mathrm{2sec}\:^{\mathrm{2}} \vartheta\:\mathrm{d}\vartheta \\ $$$$\mathrm{I}=\mathrm{8}\int\:\sqrt{\mathrm{4tan}\:^{\mathrm{2}} \vartheta+\mathrm{4}}\:\left(\mathrm{sec}\:^{\mathrm{2}} \vartheta\right)\:\mathrm{d}\vartheta \\ $$$$\mathrm{I}=\:\mathrm{16}\int\:\mathrm{sec}\:^{\mathrm{3}} \:\vartheta\mathrm{d}\vartheta \\ $$$$\mathrm{I}=\mathrm{16}\:\left\{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sec}\:\vartheta\:\mathrm{tan}\:\vartheta+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid\mathrm{sec}\:\vartheta+\mathrm{tan}\:\vartheta\mid\right\}+\:\mathrm{c} \\ $$$$\mathrm{I}=\mathrm{8}\left(\frac{\sqrt{\mathrm{t}^{\mathrm{6}} +\mathrm{4}}}{\mathrm{2}}.\:\frac{\mathrm{t}^{\mathrm{3}} }{\mathrm{2}}\right)+\mathrm{8ln}\:\mid\frac{\sqrt{\mathrm{t}^{\mathrm{6}} +\mathrm{4}}+\mathrm{t}^{\mathrm{3}} }{\mathrm{2}}\mid+\:\mathrm{c} \\ $$$$\mathrm{I}=\mathrm{2}\:\sqrt[{\mathrm{4}}]{\mathrm{x}}\:\sqrt{\mathrm{x}\sqrt{\mathrm{x}}+\mathrm{4}}\:+\:\mathrm{8ln}\:\mid\frac{\sqrt{\mathrm{x}\sqrt{\mathrm{x}}+\mathrm{4}}\:+\sqrt[{\mathrm{4}}]{\mathrm{x}}}{\mathrm{2}}\mid\:+\:\mathrm{c} \\ $$$$\mathrm{I}=\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{4}\sqrt{\mathrm{x}}}\:+\:\mathrm{8}\:\mathrm{ln}\:\mid\sqrt{\sqrt{\mathrm{x}}}\:+\sqrt{\mathrm{x}\sqrt{\mathrm{x}}+\mathrm{4}}\:\mid\:+\:\mathrm{C} \\ $$$$\mathrm{where}\:\mathrm{C}\:=\:\mathrm{c}−\mathrm{8ln}\:\left(\mathrm{2}\right) \\ $$
Commented by abdullahquwatan last updated on 06/Mar/21

$${thx}\:{sir} \\ $$
Answered by Olaf last updated on 06/Mar/21

$$\mathrm{F}\left({x}\right)\:=\:\mathrm{3}\int\sqrt{{x}+\frac{\mathrm{4}}{\:\sqrt{{x}}}}\:{dx} \\ $$$$\mathrm{Let}\:{x}\:=\:\left(\mathrm{2sh}{u}\right)^{\frac{\mathrm{4}}{\mathrm{3}}} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\mathrm{3}\int\sqrt{\left(\mathrm{2sh}{u}\right)^{\frac{\mathrm{4}}{\mathrm{3}}} +\frac{\mathrm{4}}{\:\left(\mathrm{2sh}{u}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} }}\:.\mathrm{2}^{\frac{\mathrm{4}}{\mathrm{3}}} \mathrm{ch}{u}\mathrm{sh}^{\frac{\mathrm{1}}{\mathrm{3}}} {udu} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\mathrm{3}.\mathrm{2}^{\frac{\mathrm{4}}{\mathrm{3}}} \int\frac{\mathrm{2}}{\left(\mathrm{2sh}{u}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} }\sqrt{\mathrm{sh}^{\mathrm{2}} {u}+\mathrm{1}}\:\mathrm{ch}{u}\mathrm{sh}^{\frac{\mathrm{1}}{\mathrm{3}}} {udu} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\mathrm{12}\int\mathrm{ch}^{\mathrm{2}} {udu} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\mathrm{6}\int\left(\mathrm{1}+\mathrm{ch}\left(\mathrm{2}{u}\right)\right)\:{du} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\mathrm{6}{u}+\mathrm{3sh}\left(\mathrm{2}{u}\right)+\mathrm{C} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\mathrm{6}\left({u}+\mathrm{sh}{u}\mathrm{ch}{u}\right)+\mathrm{C} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\mathrm{6}\left({u}+\mathrm{sh}{u}\sqrt{\mathrm{1}+\mathrm{sh}^{\mathrm{2}} {u}}\right)+\mathrm{C} \\ $$$${u}\:=\:\mathrm{argsh}\left(\frac{{x}^{\frac{\mathrm{3}}{\mathrm{4}}} }{\mathrm{2}}\right) \\ $$$$\mathrm{F}\left({x}\right)\:=\:\mathrm{6argsh}\left(\frac{{x}^{\frac{\mathrm{3}}{\mathrm{4}}} }{\mathrm{2}}\right)+\mathrm{3}{x}^{\frac{\mathrm{3}}{\mathrm{4}}} \sqrt{\mathrm{1}+\frac{{x}^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{4}}}+\mathrm{C} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\mathrm{6argsh}\left(\frac{{x}^{\frac{\mathrm{3}}{\mathrm{4}}} }{\mathrm{2}}\right)+\frac{\mathrm{3}}{\mathrm{2}}{x}\sqrt{{x}+\frac{\mathrm{4}}{\:\sqrt{{x}}}}+\mathrm{C} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\mathrm{6ln}\left(\frac{{x}^{\frac{\mathrm{3}}{\mathrm{4}}} }{\mathrm{2}}+\sqrt{\mathrm{1}+\frac{{x}^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{4}}}\right)+\frac{\mathrm{3}}{\mathrm{2}}{x}\sqrt{{x}+\frac{\mathrm{4}}{\:\sqrt{{x}}}}+\mathrm{C} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\mathrm{6ln}\left(\frac{{x}^{\frac{\mathrm{3}}{\mathrm{4}}} }{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}{x}^{\frac{\mathrm{1}}{\mathrm{4}}} \sqrt{{x}+\frac{\mathrm{4}}{\:\sqrt{{x}}}}\right)+\frac{\mathrm{3}}{\mathrm{2}}{x}\sqrt{{x}+\frac{\mathrm{4}}{\:\sqrt{{x}}}}+\mathrm{C} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\mathrm{6ln}\left({x}^{\frac{\mathrm{3}}{\mathrm{4}}} +{x}^{\frac{\mathrm{1}}{\mathrm{4}}} \sqrt{{x}+\frac{\mathrm{4}}{\:\sqrt{{x}}}}\right)+\frac{\mathrm{3}}{\mathrm{2}}{x}\sqrt{{x}+\frac{\mathrm{4}}{\:\sqrt{{x}}}}+\mathrm{C} \\ $$
