
Question Number 134328 by BHOOPENDRA last updated on 02/Mar/21
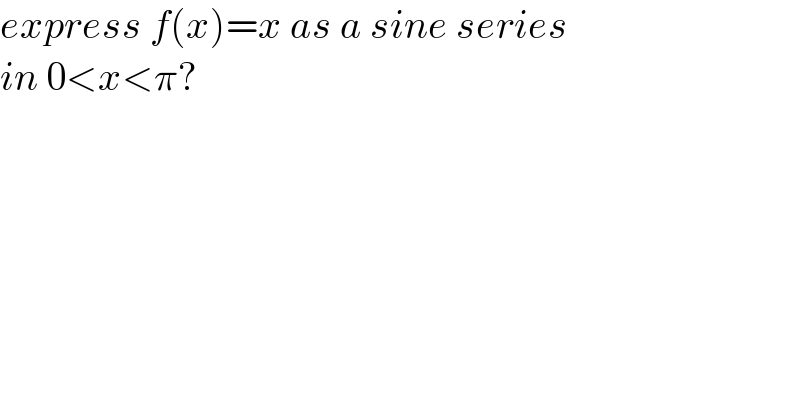
$${express}\:{f}\left({x}\right)={x}\:{as}\:{a}\:{sine}\:{series}\: \\ $$ $${in}\:\mathrm{0}<{x}<\pi? \\ $$
Answered by Dwaipayan Shikari last updated on 02/Mar/21
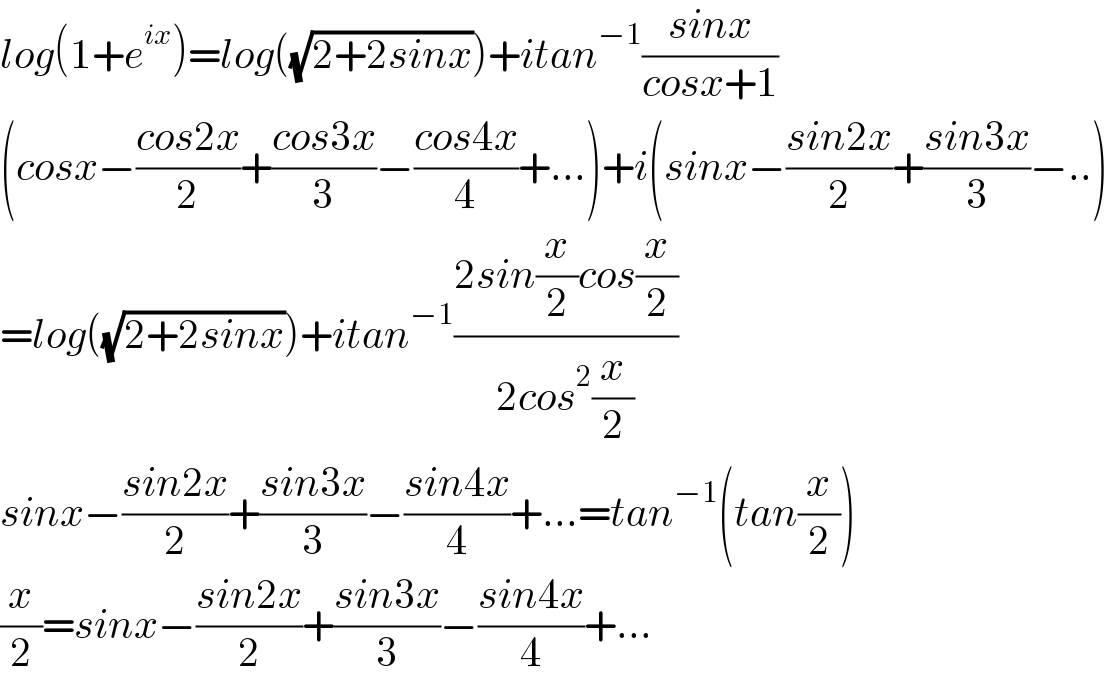
$${log}\left(\mathrm{1}+{e}^{{ix}} \right)={log}\left(\sqrt{\mathrm{2}+\mathrm{2}{sinx}}\right)+{itan}^{−\mathrm{1}} \frac{{sinx}}{{cosx}+\mathrm{1}} \\ $$ $$\left({cosx}−\frac{{cos}\mathrm{2}{x}}{\mathrm{2}}+\frac{{cos}\mathrm{3}{x}}{\mathrm{3}}−\frac{{cos}\mathrm{4}{x}}{\mathrm{4}}+...\right)+{i}\left({sinx}−\frac{{sin}\mathrm{2}{x}}{\mathrm{2}}+\frac{{sin}\mathrm{3}{x}}{\mathrm{3}}−..\right) \\ $$ $$={log}\left(\sqrt{\mathrm{2}+\mathrm{2}{sinx}}\right)+{itan}^{−\mathrm{1}} \frac{\mathrm{2}{sin}\frac{{x}}{\mathrm{2}}{cos}\frac{{x}}{\mathrm{2}}}{\mathrm{2}{cos}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}} \\ $$ $${sinx}−\frac{{sin}\mathrm{2}{x}}{\mathrm{2}}+\frac{{sin}\mathrm{3}{x}}{\mathrm{3}}−\frac{{sin}\mathrm{4}{x}}{\mathrm{4}}+...={tan}^{−\mathrm{1}} \left({tan}\frac{{x}}{\mathrm{2}}\right) \\ $$ $$\frac{{x}}{\mathrm{2}}={sinx}−\frac{{sin}\mathrm{2}{x}}{\mathrm{2}}+\frac{{sin}\mathrm{3}{x}}{\mathrm{3}}−\frac{{sin}\mathrm{4}{x}}{\mathrm{4}}+... \\ $$
Commented byDwaipayan Shikari last updated on 02/Mar/21
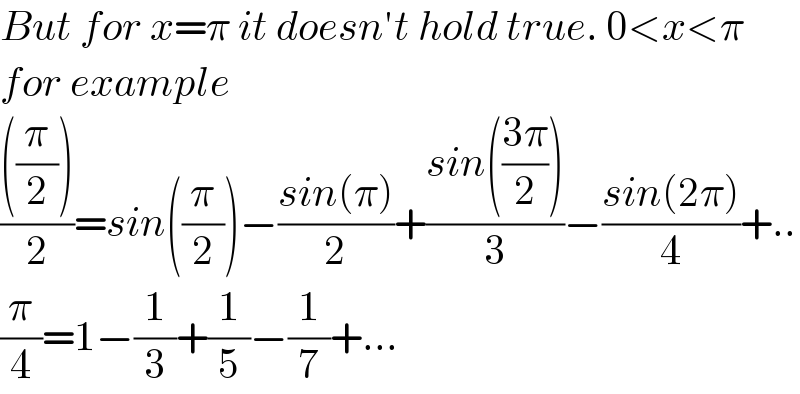
$${But}\:{for}\:{x}=\pi\:{it}\:{doesn}'{t}\:{hold}\:{true}.\:\mathrm{0}<{x}<\pi \\ $$ $${for}\:{example} \\ $$ $$\frac{\left(\frac{\pi}{\mathrm{2}}\right)}{\mathrm{2}}={sin}\left(\frac{\pi}{\mathrm{2}}\right)−\frac{{sin}\left(\pi\right)}{\mathrm{2}}+\frac{{sin}\left(\frac{\mathrm{3}\pi}{\mathrm{2}}\right)}{\mathrm{3}}−\frac{{sin}\left(\mathrm{2}\pi\right)}{\mathrm{4}}+.. \\ $$ $$\frac{\pi}{\mathrm{4}}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{7}}+... \\ $$
Commented byBHOOPENDRA last updated on 02/Mar/21

$${thanks}\:{sir} \\ $$
