
Question Number 134249 by abdurehime last updated on 01/Mar/21

Answered by mr W last updated on 01/Mar/21
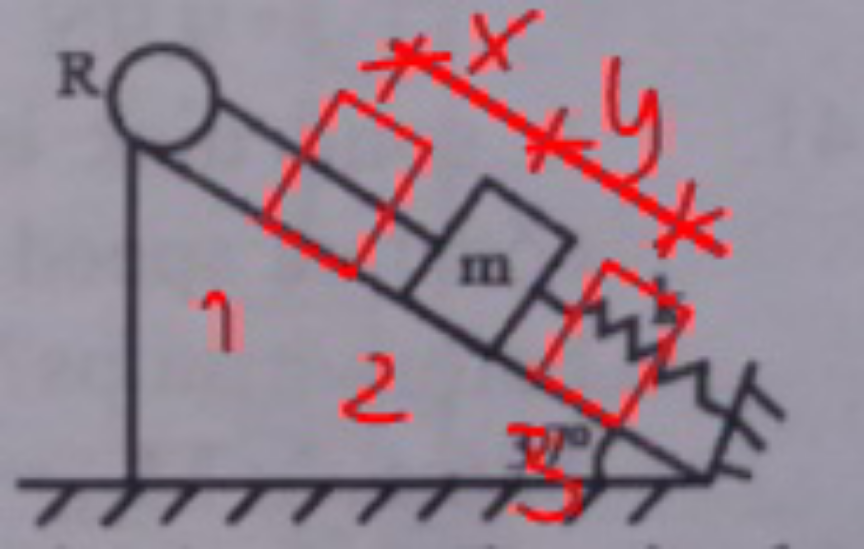
Commented by mr W last updated on 01/Mar/21

$$\mathrm{1}:\:{stretched}\:{position} \\ $$$$\mathrm{2}:\:{unstretched}\:{position}\:{of}\:{spring} \\ $$$$\mathrm{3}:\:{rest}\:{position} \\ $$$${ky}={mg}\mathrm{sin}\:\theta \\ $$$$\Rightarrow{y}=\frac{{mg}\mathrm{sin}\:\theta}{{k}} \\ $$$${at}\:{position}\:\mathrm{1}: \\ $$$${E}={mg}\left({x}+{y}\right)\mathrm{sin}\:\theta+\frac{\mathrm{1}}{\mathrm{2}}{kx}^{\mathrm{2}} \\ $$$${at}\:{position}\:\mathrm{3}: \\ $$$${E}=\frac{\mathrm{1}}{\mathrm{2}}{I}\omega^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{m}\left({R}\omega\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{ky}^{\mathrm{2}} \\ $$$$ \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{I}\omega^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{m}\left({R}\omega\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{ky}^{\mathrm{2}} ={mg}\left({x}+{y}\right)\mathrm{sin}\:\theta+\frac{\mathrm{1}}{\mathrm{2}}{kx}^{\mathrm{2}} \\ $$$$\left({I}+{mR}^{\mathrm{2}} \right)\omega^{\mathrm{2}} =\mathrm{2}{mgx}\mathrm{sin}\:\theta+{kx}^{\mathrm{2}} +\frac{\left({mg}\mathrm{sin}\:\theta\right)^{\mathrm{2}} }{{k}} \\ $$$$\omega=\sqrt{\frac{\mathrm{2}{mgx}\mathrm{sin}\:\theta+{kx}^{\mathrm{2}} +\frac{\left({mg}\mathrm{sin}\:\theta\right)^{\mathrm{2}} }{{k}}}{{I}+{mR}^{\mathrm{2}} }} \\ $$$$=\sqrt{\frac{\mathrm{2}×\mathrm{0}.\mathrm{5}×\mathrm{9}.\mathrm{71}×\mathrm{0}.\mathrm{2}×\mathrm{sin}\:\mathrm{37}°+\mathrm{50}×\mathrm{0}.\mathrm{2}^{\mathrm{2}} +\frac{\left(\mathrm{0}.\mathrm{5}×\mathrm{9}.\mathrm{81}×\mathrm{sin}\:\mathrm{37}°\right)^{\mathrm{2}} }{\mathrm{50}}}{\mathrm{1}+\mathrm{0}.\mathrm{5}×\mathrm{0}.\mathrm{3}^{\mathrm{2}} }} \\ $$$$=\mathrm{1}.\mathrm{792}\:{rad}/{s} \\ $$
