
Question Number 134122 by Ahmed1hamouda last updated on 28/Feb/21

Answered by TheSupreme last updated on 28/Feb/21
![x=1+ρcos(θ) y=ρsin(θ) z=z det(J)=ρ E={(ρ,θ,z)∣0<θ<2π , 0<ρ<1, 0<z<ρsinθ} ∫_0 ^(2π) ∫_0 ^1 ∫_0 ^(ρ sinθ) ρdzdρdθ= 2∫_0 ^π ∫_0 ^1 ρ^2 sinθdθdρ= 2[−cosθ]_0 ^π [(ρ^3 /3)]_0 ^1 =(4/3)](Q134124.png)
$${x}=\mathrm{1}+\rho{cos}\left(\theta\right) \\ $$$${y}=\rho{sin}\left(\theta\right) \\ $$$${z}={z} \\ $$$${det}\left({J}\right)=\rho \\ $$$${E}=\left\{\left(\rho,\theta,{z}\right)\mid\mathrm{0}<\theta<\mathrm{2}\pi\:,\:\mathrm{0}<\rho<\mathrm{1},\:\mathrm{0}<{z}<\rho{sin}\theta\right\} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} \int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\rho\:{sin}\theta} \rho{dzd}\rho{d}\theta= \\ $$$$\mathrm{2}\int_{\mathrm{0}} ^{\pi} \int_{\mathrm{0}} ^{\mathrm{1}} \rho^{\mathrm{2}} {sin}\theta{d}\theta{d}\rho= \\ $$$$\mathrm{2}\left[−{cos}\theta\right]_{\mathrm{0}} ^{\pi} \left[\frac{\rho^{\mathrm{3}} }{\mathrm{3}}\right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{4}}{\mathrm{3}} \\ $$
Commented by Ahmed1hamouda last updated on 28/Feb/21
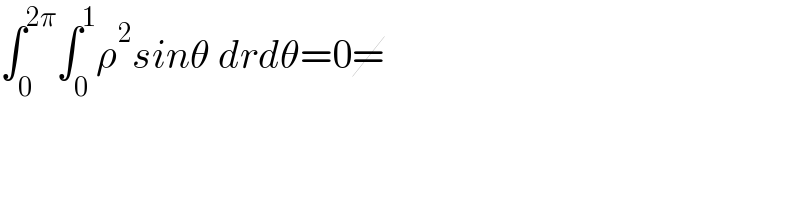
$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} \int_{\mathrm{0}} ^{\mathrm{1}} \rho^{\mathrm{2}} {sin}\theta\:{drd}\theta=\mathrm{0}\cancel{=} \\ $$
