
Question Number 134070 by mohammad17 last updated on 27/Feb/21

$$\int_{\mathrm{0}} ^{\:{x}} \left({x}−{t}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \left({t}\right)^{\frac{\mathrm{5}}{\mathrm{2}}} {dt} \\ $$
Commented by mohammad17 last updated on 27/Feb/21

$${help}\:{me}\:{sir} \\ $$
Answered by Dwaipayan Shikari last updated on 27/Feb/21
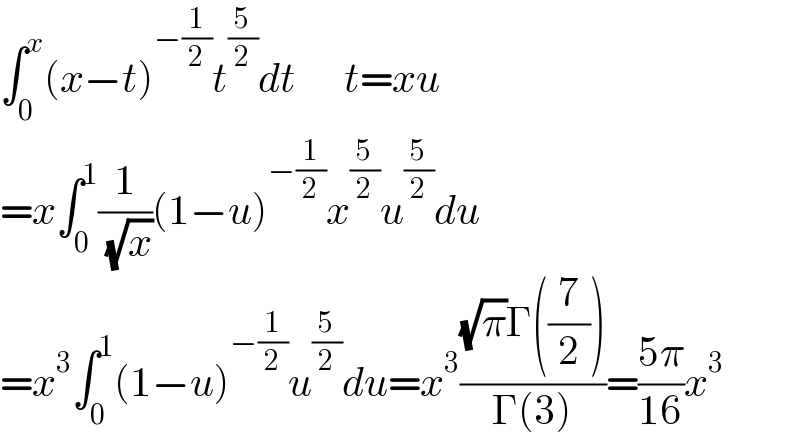
$$\int_{\mathrm{0}} ^{{x}} \left({x}−{t}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} {t}^{\frac{\mathrm{5}}{\mathrm{2}}} {dt}\:\:\:\:\:\:{t}={xu} \\ $$$$={x}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{{x}}}\left(\mathrm{1}−{u}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} {x}^{\frac{\mathrm{5}}{\mathrm{2}}} {u}^{\frac{\mathrm{5}}{\mathrm{2}}} {du} \\ $$$$={x}^{\mathrm{3}} \int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{u}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} {u}^{\frac{\mathrm{5}}{\mathrm{2}}} {du}={x}^{\mathrm{3}} \frac{\sqrt{\pi}\Gamma\left(\frac{\mathrm{7}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{3}\right)}=\frac{\mathrm{5}\pi}{\mathrm{16}}{x}^{\mathrm{3}} \\ $$
Answered by mathmax by abdo last updated on 27/Feb/21
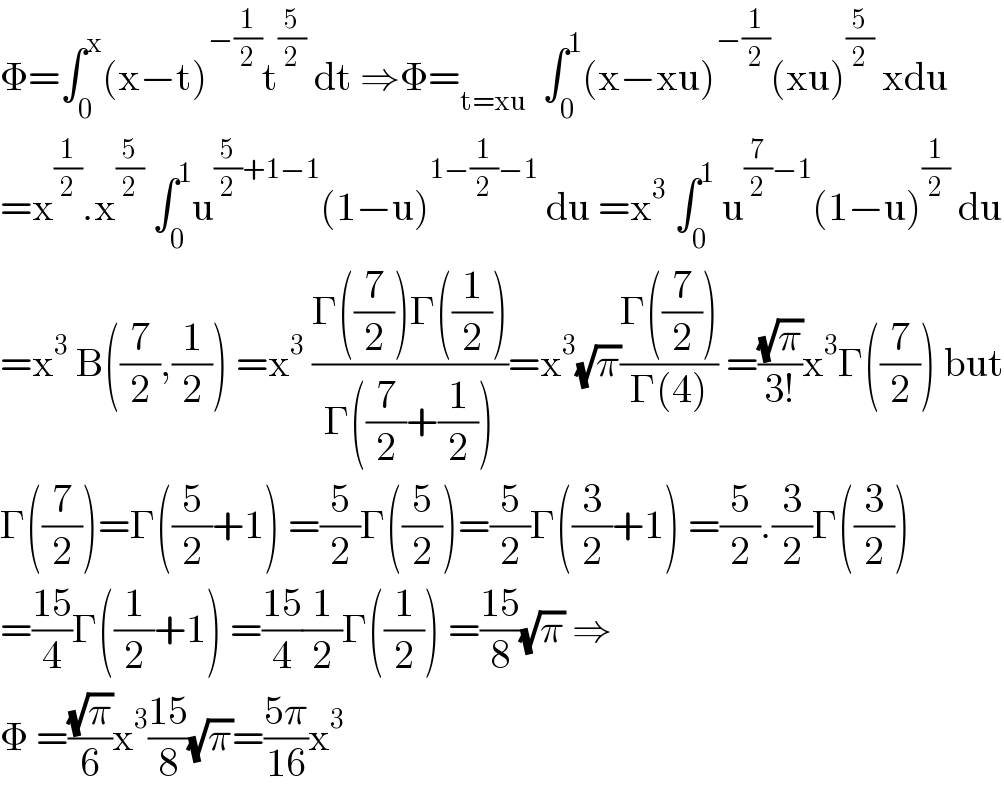
$$\Phi=\int_{\mathrm{0}} ^{\mathrm{x}} \left(\mathrm{x}−\mathrm{t}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{t}^{\frac{\mathrm{5}}{\mathrm{2}}} \:\mathrm{dt}\:\Rightarrow\Phi=_{\mathrm{t}=\mathrm{xu}} \:\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{x}−\mathrm{xu}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{xu}\right)^{\frac{\mathrm{5}}{\mathrm{2}}} \:\mathrm{xdu} \\ $$$$=\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{2}}} .\mathrm{x}^{\frac{\mathrm{5}}{\mathrm{2}}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{u}^{\frac{\mathrm{5}}{\mathrm{2}}+\mathrm{1}−\mathrm{1}} \left(\mathrm{1}−\mathrm{u}\right)^{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} \:\mathrm{du}\:=\mathrm{x}^{\mathrm{3}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{u}^{\frac{\mathrm{7}}{\mathrm{2}}−\mathrm{1}} \left(\mathrm{1}−\mathrm{u}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{du} \\ $$$$=\mathrm{x}^{\mathrm{3}} \:\mathrm{B}\left(\frac{\mathrm{7}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\mathrm{x}^{\mathrm{3}} \:\frac{\Gamma\left(\frac{\mathrm{7}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\frac{\mathrm{7}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right)}=\mathrm{x}^{\mathrm{3}} \sqrt{\pi}\frac{\Gamma\left(\frac{\mathrm{7}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{4}\right)}\:=\frac{\sqrt{\pi}}{\mathrm{3}!}\mathrm{x}^{\mathrm{3}} \Gamma\left(\frac{\mathrm{7}}{\mathrm{2}}\right)\:\mathrm{but} \\ $$$$\Gamma\left(\frac{\mathrm{7}}{\mathrm{2}}\right)=\Gamma\left(\frac{\mathrm{5}}{\mathrm{2}}+\mathrm{1}\right)\:=\frac{\mathrm{5}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{5}}{\mathrm{2}}\right)=\frac{\mathrm{5}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}+\mathrm{1}\right)\:=\frac{\mathrm{5}}{\mathrm{2}}.\frac{\mathrm{3}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{15}}{\mathrm{4}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{1}\right)\:=\frac{\mathrm{15}}{\mathrm{4}}\frac{\mathrm{1}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\frac{\mathrm{15}}{\mathrm{8}}\sqrt{\pi}\:\Rightarrow \\ $$$$\Phi\:=\frac{\sqrt{\pi}}{\mathrm{6}}\mathrm{x}^{\mathrm{3}} \frac{\mathrm{15}}{\mathrm{8}}\sqrt{\pi}=\frac{\mathrm{5}\pi}{\mathrm{16}}\mathrm{x}^{\mathrm{3}} \\ $$
