Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 13388 by Tinkutara last updated on 19/May/17

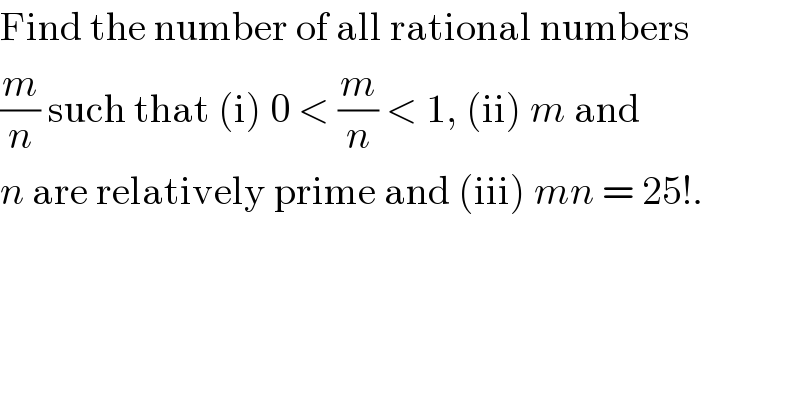
Find the number of all rational numbers (m/n) such that (i) 0 < (m/n) < 1, (ii) m and n are relatively prime and (iii) mn = 25!.

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{all}\:\mathrm{rational}\:\mathrm{numbers} \\ $$ $$\frac{{m}}{{n}}\:\mathrm{such}\:\mathrm{that}\:\left(\mathrm{i}\right)\:\mathrm{0}\:<\:\frac{{m}}{{n}}\:<\:\mathrm{1},\:\left(\mathrm{ii}\right)\:{m}\:\mathrm{and} \\ $$ $${n}\:\mathrm{are}\:\mathrm{relatively}\:\mathrm{prime}\:\mathrm{and}\:\left(\mathrm{iii}\right)\:{mn}\:=\:\mathrm{25}!. \\ $$

Commented byRasheedSindhi last updated on 19/May/17

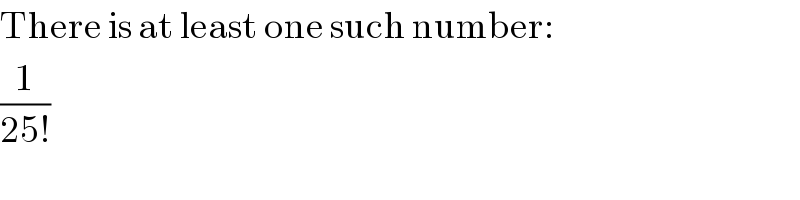
There is at least one such number: (1/(25!))

$$\mathrm{There}\:\mathrm{is}\:\mathrm{at}\:\mathrm{least}\:\mathrm{one}\:\mathrm{such}\:\mathrm{number}: \\ $$ $$\frac{\mathrm{1}}{\mathrm{25}!} \\ $$

Commented byprakash jain last updated on 19/May/17

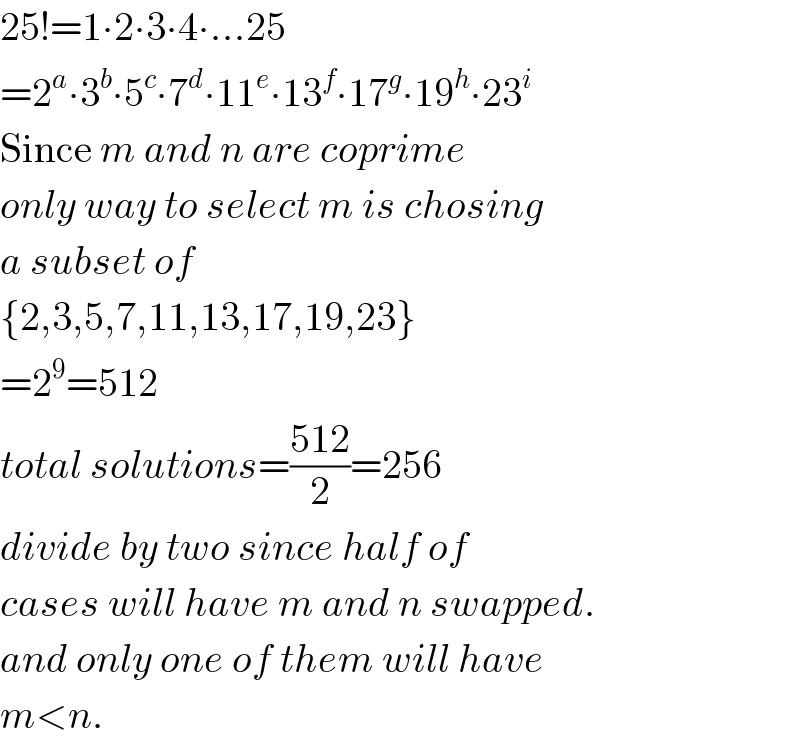
25!=1∙2∙3∙4∙...25 =2^a ∙3^b ∙5^c ∙7^d ∙11^e ∙13^f ∙17^g ∙19^h ∙23^i Since m and n are coprime only way to select m is chosing a subset of {2,3,5,7,11,13,17,19,23} =2^9 =512 total solutions=((512)/2)=256 divide by two since half of cases will have m and n swapped. and only one of them will have m<n.

$$\mathrm{25}!=\mathrm{1}\centerdot\mathrm{2}\centerdot\mathrm{3}\centerdot\mathrm{4}\centerdot...\mathrm{25} \\ $$ $$=\mathrm{2}^{{a}} \centerdot\mathrm{3}^{{b}} \centerdot\mathrm{5}^{{c}} \centerdot\mathrm{7}^{{d}} \centerdot\mathrm{11}^{{e}} \centerdot\mathrm{13}^{{f}} \centerdot\mathrm{17}^{{g}} \centerdot\mathrm{19}^{{h}} \centerdot\mathrm{23}^{{i}} \\ $$ $$\mathrm{Since}\:{m}\:{and}\:{n}\:{are}\:{coprime} \\ $$ $${only}\:{way}\:{to}\:{select}\:{m}\:{is}\:{chosing} \\ $$ $${a}\:{subset}\:{of}\: \\ $$ $$\left\{\mathrm{2},\mathrm{3},\mathrm{5},\mathrm{7},\mathrm{11},\mathrm{13},\mathrm{17},\mathrm{19},\mathrm{23}\right\} \\ $$ $$=\mathrm{2}^{\mathrm{9}} =\mathrm{512} \\ $$ $${total}\:{solutions}=\frac{\mathrm{512}}{\mathrm{2}}=\mathrm{256} \\ $$ $${divide}\:{by}\:{two}\:{since}\:{half}\:{of} \\ $$ $${cases}\:{will}\:{have}\:{m}\:{and}\:{n}\:{swapped}. \\ $$ $${and}\:{only}\:{one}\:{of}\:{them}\:{will}\:{have} \\ $$ $${m}<{n}. \\ $$

Commented bymrW1 last updated on 20/May/17

how is to understand the condiction that m and n are relatively prime?

$${how}\:{is}\:{to}\:{understand}\:{the}\:{condiction} \\ $$ $${that}\:{m}\:{and}\:{n}\:{are}\:{relatively}\:{prime}? \\ $$

Commented byprakash jain last updated on 20/May/17

Since m and n are relatively prime and distinct prime factor of 25! are {2, 3, 5, 7, 11, 13, 17, 19, 23} we chose of subset of above set say {2,3,5} m=2^a 3^b 5^c n=7^d 11^e 13^f 17^g 19^h 23^i so m and n are relative prime. but when we select m=7^d 11^e 13^f 17^g 19^h 23^i n=2^a 3^b 5^c we discard one of the choice so divide by 2.

$$\mathrm{Since}\:{m}\:\mathrm{and}\:{n}\:\mathrm{are}\:\mathrm{relatively}\:\mathrm{prime} \\ $$ $$\mathrm{and}\:\mathrm{distinct}\:\mathrm{prime}\:\mathrm{factor}\:\mathrm{of}\:\mathrm{25}!\:\mathrm{are} \\ $$ $$\left\{\mathrm{2},\:\mathrm{3},\:\mathrm{5},\:\mathrm{7},\:\mathrm{11},\:\mathrm{13},\:\mathrm{17},\:\mathrm{19},\:\mathrm{23}\right\} \\ $$ $$\mathrm{we}\:\mathrm{chose}\:\mathrm{of}\:\mathrm{subset}\:\mathrm{of}\:\mathrm{above}\:\mathrm{set} \\ $$ $$\mathrm{say}\:\left\{\mathrm{2},\mathrm{3},\mathrm{5}\right\} \\ $$ $${m}=\mathrm{2}^{{a}} \mathrm{3}^{{b}} \mathrm{5}^{{c}} \\ $$ $${n}=\mathrm{7}^{{d}} \mathrm{11}^{{e}} \mathrm{13}^{{f}} \mathrm{17}^{{g}} \mathrm{19}^{{h}} \mathrm{23}^{{i}} \\ $$ $$\mathrm{so}\:{m}\:\mathrm{and}\:{n}\:\mathrm{are}\:\mathrm{relative}\:\mathrm{prime}. \\ $$ $$\mathrm{but}\:\mathrm{when}\:\mathrm{we}\:\mathrm{select} \\ $$ $${m}=\mathrm{7}^{{d}} \mathrm{11}^{{e}} \mathrm{13}^{{f}} \mathrm{17}^{{g}} \mathrm{19}^{{h}} \mathrm{23}^{{i}} \\ $$ $${n}=\mathrm{2}^{{a}} \mathrm{3}^{{b}} \mathrm{5}^{{c}} \\ $$ $$\mathrm{we}\:\mathrm{discard}\:\mathrm{one}\:\mathrm{of}\:\mathrm{the}\:\mathrm{choice}\:\mathrm{so}\:\mathrm{divide}\:\mathrm{by}\:\mathrm{2}. \\ $$

Commented bymrW1 last updated on 20/May/17

Thanks!

$${Thanks}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com