
Question Number 133791 by mnjuly1970 last updated on 24/Feb/21
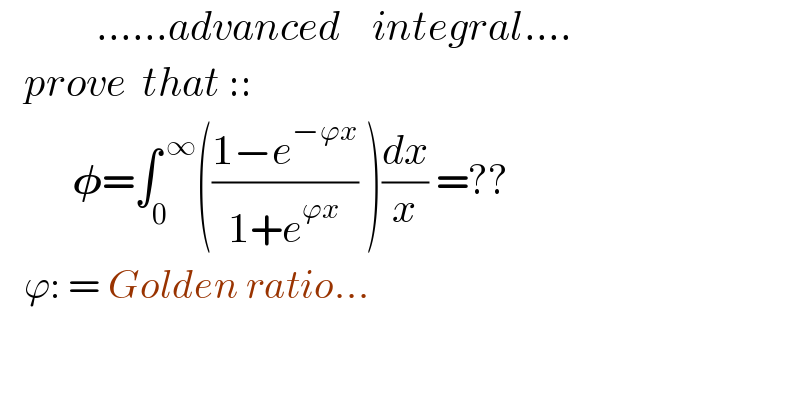
$$\:\:\:\:\:\:\:\:\:\:\:\:......{advanced}\:\:\:\:{integral}.... \\ $$$$\:\:\:{prove}\:\:{that}\::: \\ $$$$\:\:\:\:\:\:\:\:\:\boldsymbol{\phi}=\int_{\mathrm{0}} ^{\:\infty} \left(\frac{\mathrm{1}−{e}^{−\varphi{x}} }{\mathrm{1}+{e}^{\varphi{x}} }\:\right)\frac{{dx}}{{x}}\:=?? \\ $$$$\:\:\:\varphi:\:=\:{Golden}\:{ratio}... \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 24/Feb/21
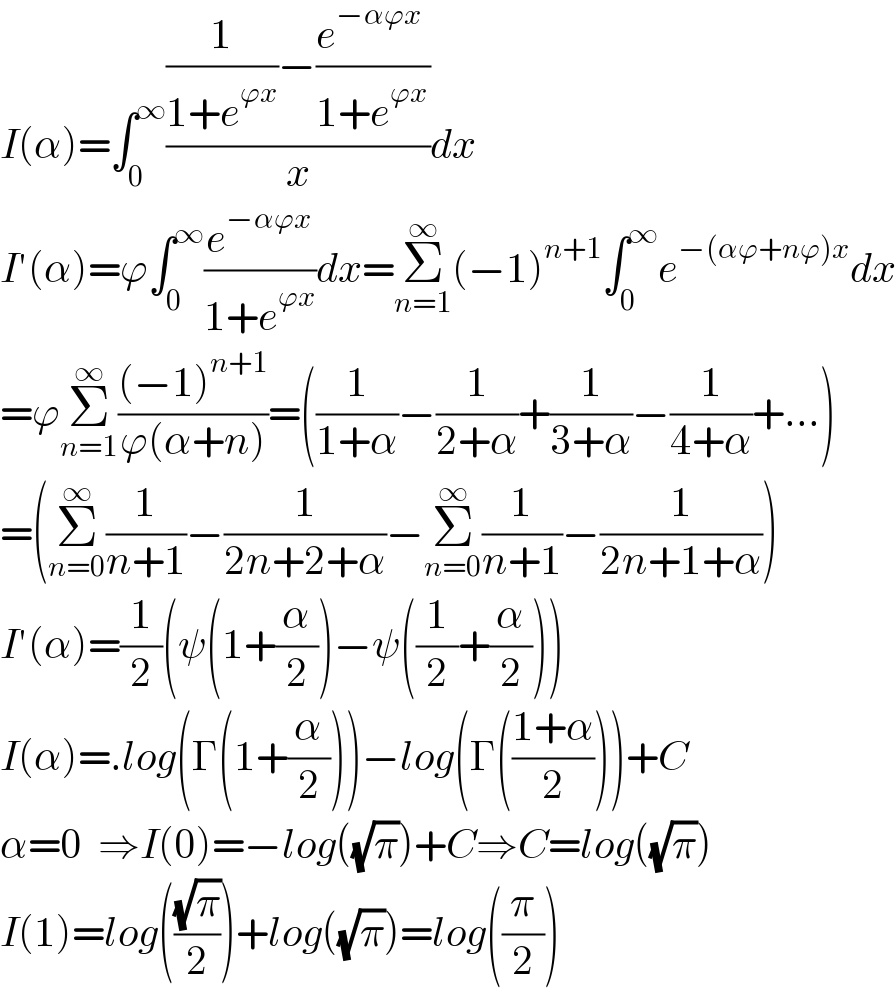
$${I}\left(\alpha\right)=\int_{\mathrm{0}} ^{\infty} \frac{\frac{\mathrm{1}}{\mathrm{1}+{e}^{\varphi{x}} }−\frac{{e}^{−\alpha\varphi{x}} \:}{\mathrm{1}+{e}^{\varphi{x}} }}{{x}}{dx} \\ $$$${I}'\left(\alpha\right)=\varphi\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−\alpha\varphi{x}} }{\mathrm{1}+{e}^{\varphi{x}} }{dx}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \int_{\mathrm{0}} ^{\infty} {e}^{−\left(\alpha\varphi+{n}\varphi\right){x}} {dx} \\ $$$$=\varphi\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\varphi\left(\alpha+{n}\right)}=\left(\frac{\mathrm{1}}{\mathrm{1}+\alpha}−\frac{\mathrm{1}}{\mathrm{2}+\alpha}+\frac{\mathrm{1}}{\mathrm{3}+\alpha}−\frac{\mathrm{1}}{\mathrm{4}+\alpha}+...\right) \\ $$$$=\left(\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{2}+\alpha}−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}+\alpha}\right) \\ $$$${I}'\left(\alpha\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\psi\left(\mathrm{1}+\frac{\alpha}{\mathrm{2}}\right)−\psi\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\alpha}{\mathrm{2}}\right)\right) \\ $$$${I}\left(\alpha\right)=.{log}\left(\Gamma\left(\mathrm{1}+\frac{\alpha}{\mathrm{2}}\right)\right)−{log}\left(\Gamma\left(\frac{\mathrm{1}+\alpha}{\mathrm{2}}\right)\right)+{C} \\ $$$$\alpha=\mathrm{0}\:\:\Rightarrow{I}\left(\mathrm{0}\right)=−{log}\left(\sqrt{\pi}\right)+{C}\Rightarrow{C}={log}\left(\sqrt{\pi}\right) \\ $$$${I}\left(\mathrm{1}\right)={log}\left(\frac{\sqrt{\pi}}{\mathrm{2}}\right)+{log}\left(\sqrt{\pi}\right)={log}\left(\frac{\pi}{\mathrm{2}}\right) \\ $$
Commented by Dwaipayan Shikari last updated on 24/Feb/21
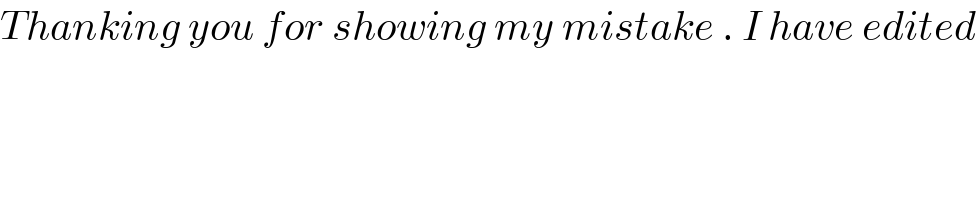
$${Thanking}\:{you}\:{for}\:{showing}\:{my}\:{mistake}\:.\:{I}\:{have}\:{edited} \\ $$
Commented by mnjuly1970 last updated on 24/Feb/21

$${grateful}... \\ $$
Commented by mathDivergent last updated on 24/Feb/21

Commented by mathDivergent last updated on 24/Feb/21
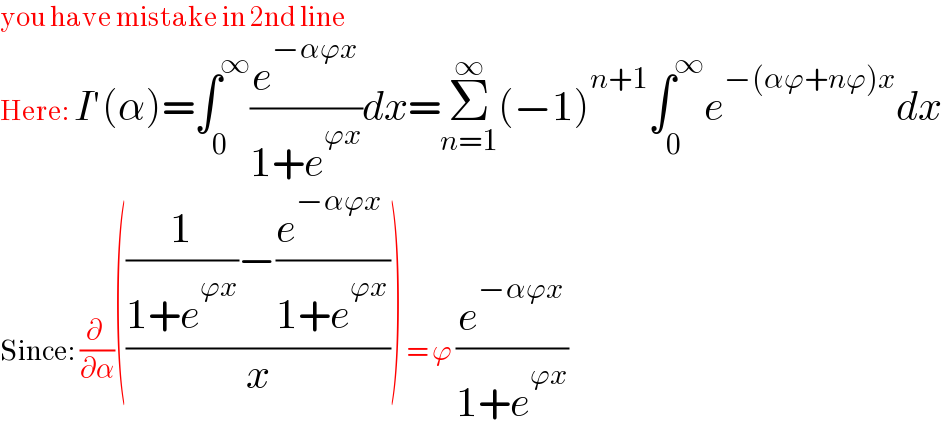
$$\mathrm{you}\:\mathrm{have}\:\mathrm{mistake}\:\mathrm{in}\:\mathrm{2nd}\:\mathrm{line} \\ $$$$\mathrm{Here}:\:{I}'\left(\alpha\right)=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−\alpha\varphi{x}} }{\mathrm{1}+{e}^{\varphi{x}} }{dx}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \int_{\mathrm{0}} ^{\infty} {e}^{−\left(\alpha\varphi+{n}\varphi\right){x}} {dx} \\ $$$$\mathrm{Since}:\:\frac{\partial\:}{\partial\alpha}\left(\frac{\frac{\mathrm{1}}{\mathrm{1}+{e}^{\varphi{x}} }−\frac{{e}^{−\alpha\varphi{x}} \:}{\mathrm{1}+{e}^{\varphi{x}} }}{{x}}\right)\:=\:\varphi\:\frac{{e}^{−\alpha\varphi{x}} }{\mathrm{1}+{e}^{\varphi{x}} } \\ $$
Commented by mathDivergent last updated on 24/Feb/21
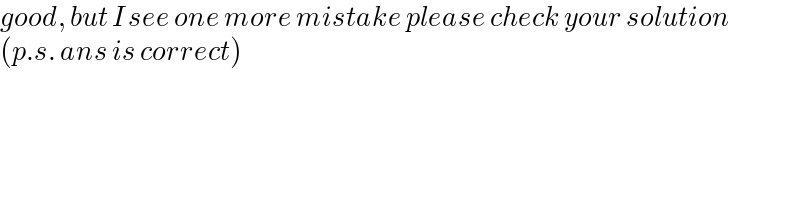
$${good},\:{but}\:{I}\:{see}\:{one}\:{more}\:{mistake}\:{please}\:{check}\:{your}\:{solution} \\ $$$$\left({p}.{s}.\:{ans}\:{is}\:{correct}\right) \\ $$
Answered by mathDivergent last updated on 24/Feb/21

$$\:\:\:\:\mathrm{ln}\:\frac{\pi}{\mathrm{2}} \\ $$
