
Question Number 133616 by benjo_mathlover last updated on 23/Feb/21

$$\mathrm{Suppose}\:\mathrm{function}\:\mathrm{f}:\mathrm{R}\rightarrow\mathrm{R}\:\mathrm{with} \\ $$$$\mathrm{f}\left(\mathrm{2x}−\mathrm{3}\right)\:=\:\mathrm{4x}^{\mathrm{2}} +\mathrm{2x}−\mathrm{5}\:\mathrm{and}\:\mathrm{f}\:'\:\mathrm{denote} \\ $$$$\mathrm{is}\:\mathrm{derivatif}\:\mathrm{of}\:\mathrm{f}\:\mathrm{function}. \\ $$$$\mathrm{What}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{f}\:'\left(\mathrm{2x}−\mathrm{3}\right) \\ $$
Commented by mr W last updated on 23/Feb/21

$$\mathrm{4}{x}+\mathrm{1} \\ $$
Answered by TheSupreme last updated on 23/Feb/21
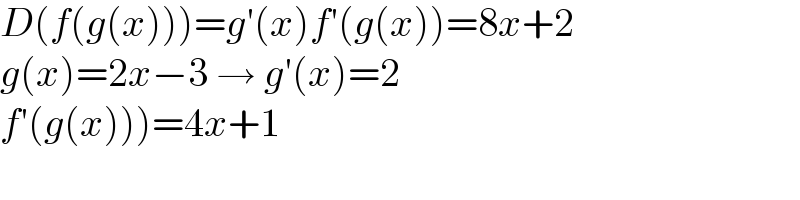
$${D}\left({f}\left({g}\left({x}\right)\right)\right)={g}'\left({x}\right){f}'\left({g}\left({x}\right)\right)=\mathrm{8}{x}+\mathrm{2} \\ $$$${g}\left({x}\right)=\mathrm{2}{x}−\mathrm{3}\:\rightarrow\:{g}'\left({x}\right)=\mathrm{2} \\ $$$$\left.{f}'\left({g}\left({x}\right)\right)\right)=\mathrm{4}{x}+\mathrm{1} \\ $$
Answered by liberty last updated on 23/Feb/21
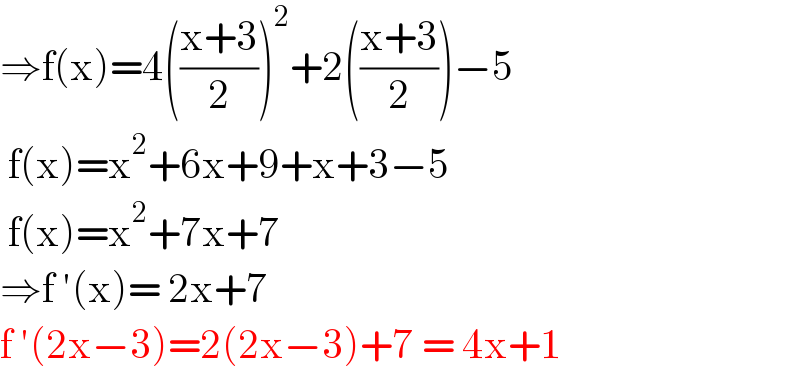
$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mathrm{4}\left(\frac{\mathrm{x}+\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{2}\left(\frac{\mathrm{x}+\mathrm{3}}{\mathrm{2}}\right)−\mathrm{5} \\ $$$$\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{2}} +\mathrm{6x}+\mathrm{9}+\mathrm{x}+\mathrm{3}−\mathrm{5} \\ $$$$\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{2}} +\mathrm{7x}+\mathrm{7}\: \\ $$$$\Rightarrow\mathrm{f}\:'\left(\mathrm{x}\right)=\:\mathrm{2x}+\mathrm{7} \\ $$$$\mathrm{f}\:'\left(\mathrm{2x}−\mathrm{3}\right)=\mathrm{2}\left(\mathrm{2x}−\mathrm{3}\right)+\mathrm{7}\:=\:\mathrm{4x}+\mathrm{1}\: \\ $$
Answered by mr W last updated on 23/Feb/21
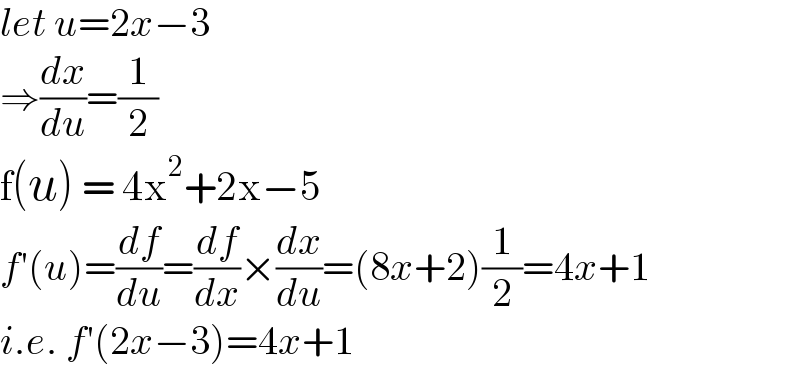
$${let}\:{u}=\mathrm{2}{x}−\mathrm{3} \\ $$$$\Rightarrow\frac{{dx}}{{du}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{f}\left({u}\right)\:=\:\mathrm{4x}^{\mathrm{2}} +\mathrm{2x}−\mathrm{5} \\ $$$${f}'\left({u}\right)=\frac{{df}}{{du}}=\frac{{df}}{{dx}}×\frac{{dx}}{{du}}=\left(\mathrm{8}{x}+\mathrm{2}\right)\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{4}{x}+\mathrm{1} \\ $$$${i}.{e}.\:{f}'\left(\mathrm{2}{x}−\mathrm{3}\right)=\mathrm{4}{x}+\mathrm{1} \\ $$
