
Question Number 133615 by benjo_mathlover last updated on 23/Feb/21
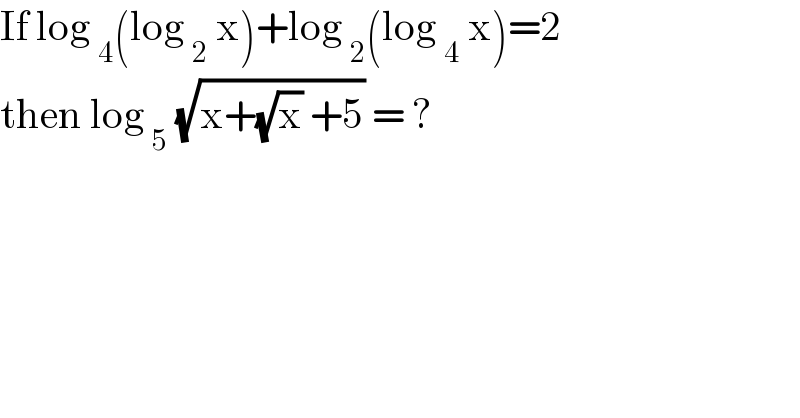
$$\mathrm{If}\:\mathrm{log}\:_{\mathrm{4}} \left(\mathrm{log}\:_{\mathrm{2}} \:\mathrm{x}\right)+\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{log}\:_{\mathrm{4}} \:\mathrm{x}\right)=\mathrm{2} \\ $$$$\mathrm{then}\:\mathrm{log}\:_{\mathrm{5}} \:\sqrt{\mathrm{x}+\sqrt{\mathrm{x}}\:+\mathrm{5}}\:=\:? \\ $$
Answered by TheSupreme last updated on 23/Feb/21
![log_4 (x)=((log_2 x)/(log_2 4))=(1/2)log_2 x (1/2)log_2 (log_2 (x))+log_2 ((1/2)log_2 (x))=2 log_2 [(1/2)log_2 (x)^(3/2) ]=2 (1/2)log^(3/2) (x)=4 log^(3/2) (x)=8 → log_2 (x)=2^(3×(2/3)) =4 x=2^4 =16 log_5 ((√(16+(√(16))+5)))=log_5 (25)=2](Q133623.png)
$${log}_{\mathrm{4}} \left({x}\right)=\frac{{log}_{\mathrm{2}} {x}}{{log}_{\mathrm{2}} \mathrm{4}}=\frac{\mathrm{1}}{\mathrm{2}}{log}_{\mathrm{2}} {x} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{log}_{\mathrm{2}} \left({log}_{\mathrm{2}} \left({x}\right)\right)+{log}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}{log}_{\mathrm{2}} \left({x}\right)\right)=\mathrm{2} \\ $$$${log}_{\mathrm{2}} \left[\frac{\mathrm{1}}{\mathrm{2}}{log}_{\mathrm{2}} \left({x}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \right]=\mathrm{2} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{log}^{\frac{\mathrm{3}}{\mathrm{2}}} \left({x}\right)=\mathrm{4} \\ $$$${log}^{\frac{\mathrm{3}}{\mathrm{2}}} \left({x}\right)=\mathrm{8}\:\rightarrow\:{log}_{\mathrm{2}} \left({x}\right)=\mathrm{2}^{\mathrm{3}×\frac{\mathrm{2}}{\mathrm{3}}} =\mathrm{4} \\ $$$${x}=\mathrm{2}^{\mathrm{4}} =\mathrm{16} \\ $$$${log}_{\mathrm{5}} \left(\sqrt{\mathrm{16}+\sqrt{\mathrm{16}}+\mathrm{5}}\right)={log}_{\mathrm{5}} \left(\mathrm{25}\right)=\mathrm{2} \\ $$
Commented by JDamian last updated on 24/Feb/21

$$\sqrt{\mathrm{16}+\sqrt{\mathrm{16}}+\mathrm{5}}\:\neq\:\mathrm{25} \\ $$$$\sqrt{\mathrm{16}+\sqrt{\mathrm{16}}+\mathrm{5}\:}=\:\sqrt{\mathrm{25}}=\mathrm{5} \\ $$
Answered by liberty last updated on 25/Feb/21
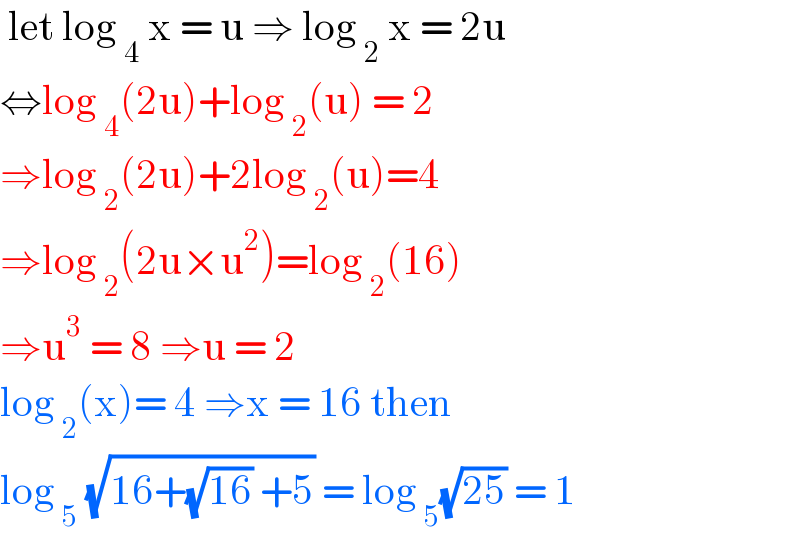
$$\:\mathrm{let}\:\mathrm{log}\:_{\mathrm{4}} \:\mathrm{x}\:=\:\mathrm{u}\:\Rightarrow\:\mathrm{log}\:_{\mathrm{2}} \:\mathrm{x}\:=\:\mathrm{2u} \\ $$$$\Leftrightarrow\mathrm{log}\:_{\mathrm{4}} \left(\mathrm{2u}\right)+\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{u}\right)\:=\:\mathrm{2} \\ $$$$\Rightarrow\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{2u}\right)+\mathrm{2log}\:_{\mathrm{2}} \left(\mathrm{u}\right)=\mathrm{4} \\ $$$$\Rightarrow\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{2u}×\mathrm{u}^{\mathrm{2}} \right)=\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{16}\right) \\ $$$$\Rightarrow\mathrm{u}^{\mathrm{3}} \:=\:\mathrm{8}\:\Rightarrow\mathrm{u}\:=\:\mathrm{2} \\ $$$$\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{x}\right)=\:\mathrm{4}\:\Rightarrow\mathrm{x}\:=\:\mathrm{16}\:\mathrm{then}\: \\ $$$$\mathrm{log}\:_{\mathrm{5}} \:\sqrt{\mathrm{16}+\sqrt{\mathrm{16}}\:+\mathrm{5}}\:=\:\mathrm{log}\:_{\mathrm{5}} \sqrt{\mathrm{25}}\:=\:\mathrm{1} \\ $$
Commented by JDamian last updated on 24/Feb/21
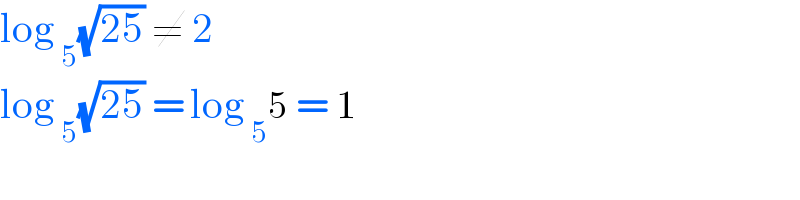
$$\mathrm{log}\:_{\mathrm{5}} \sqrt{\mathrm{25}}\:\neq\:\mathrm{2} \\ $$$$\mathrm{log}\:_{\mathrm{5}} \sqrt{\mathrm{25}}\:=\:\mathrm{log}\:_{\mathrm{5}} \mathrm{5}\:=\:\mathrm{1} \\ $$
