
Question Number 133530 by snipers237 last updated on 22/Feb/21
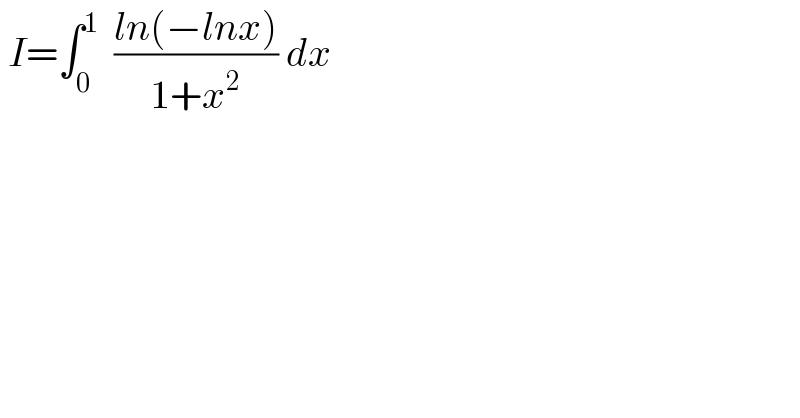
$$\:{I}=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{ln}\left(−{lnx}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}\: \\ $$
Commented by Dwaipayan Shikari last updated on 22/Feb/21
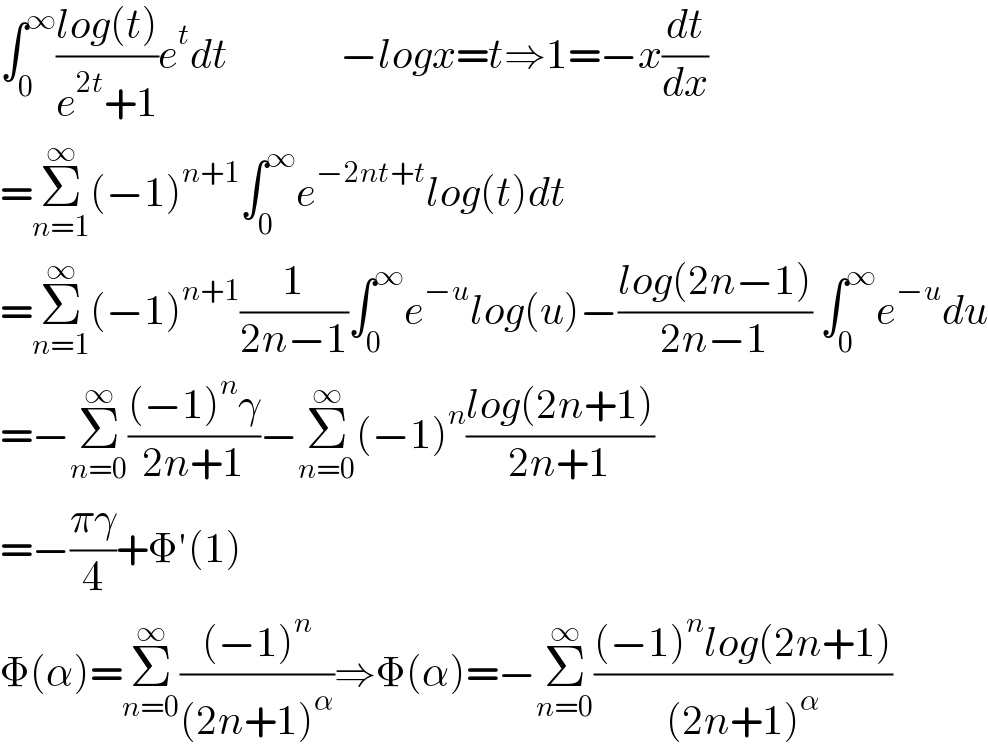
$$\int_{\mathrm{0}} ^{\infty} \frac{{log}\left({t}\right)}{{e}^{\mathrm{2}{t}} +\mathrm{1}}{e}^{{t}} {dt}\:\:\:\:\:\:\:\:\:\:\:\:\:\:−{logx}={t}\Rightarrow\mathrm{1}=−{x}\frac{{dt}}{{dx}} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{2}{nt}+{t}} {log}\left({t}\right){dt} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}}\int_{\mathrm{0}} ^{\infty} {e}^{−{u}} {log}\left({u}\right)−\frac{{log}\left(\mathrm{2}{n}−\mathrm{1}\right)}{\mathrm{2}{n}−\mathrm{1}}\:\int_{\mathrm{0}} ^{\infty} {e}^{−{u}} {du} \\ $$$$=−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} \gamma}{\mathrm{2}{n}+\mathrm{1}}−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{{log}\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{2}{n}+\mathrm{1}} \\ $$$$=−\frac{\pi\gamma}{\mathrm{4}}+\Phi'\left(\mathrm{1}\right) \\ $$$$\Phi\left(\alpha\right)=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\alpha} }\Rightarrow\Phi\left(\alpha\right)=−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} {log}\left(\mathrm{2}{n}+\mathrm{1}\right)}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\alpha} } \\ $$
Commented by snipers237 last updated on 23/Feb/21
![thanks for crying sir , but i think if x∈[0,1] then i can write (1/(1+x^2 ))=Σ_(n=0) ^∞ (−x^2 )^n but when t∈[0,∞[ , we have e^t ∈[1,∞[ , so you can′t replace x by e^t in the previous equality you could thing about dividing by e^(2t) the numerator and the denominator in the way to get ∫_0 ^∞ ((e^(−t) lnt)/(1+e^(−2t) ))dt before replacing x by e^(−2t)](Q133578.png)
$${thanks}\:{for}\:{crying}\:{sir}\:,\:{but}\:{i}\:{think} \\ $$$${if}\:{x}\in\left[\mathrm{0},\mathrm{1}\right]\:{then}\:{i}\:{can}\:{write}\:\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−{x}^{\mathrm{2}} \right)^{{n}} \: \\ $$$${but}\:{when}\:{t}\in\left[\mathrm{0},\infty\left[\:,\:{we}\:{have}\:{e}^{{t}} \in\left[\mathrm{1},\infty\left[\:,\:{so}\:{you}\:{can}'{t}\:{replace}\:{x}\:{by}\:{e}^{{t}} \:{in}\:{the}\:{previous}\:{equality}\:\right.\right.\right.\right. \\ $$$${you}\:{could}\:{thing}\:{about}\:{dividing}\:{by}\:\:{e}^{\mathrm{2}{t}} \:\:\:{the}\:{numerator}\:{and}\:{the}\:{denominator}\:{in}\:{the}\:{way}\:{to}\:{get}\: \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{t}} {lnt}}{\mathrm{1}+{e}^{−\mathrm{2}{t}} }{dt}\:\:\:\:{before}\:{replacing}\:{x}\:{by}\:{e}^{−\mathrm{2}{t}} \\ $$$$ \\ $$
Commented by Dwaipayan Shikari last updated on 23/Feb/21
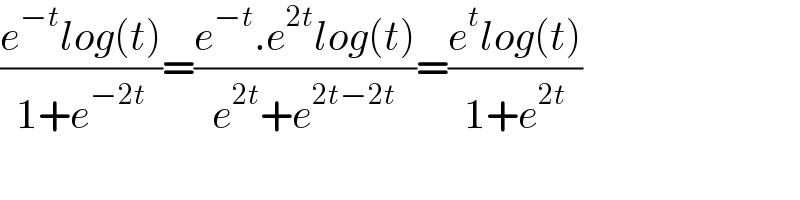
$$\frac{{e}^{−{t}} {log}\left({t}\right)}{\mathrm{1}+{e}^{−\mathrm{2}{t}} }=\frac{{e}^{−{t}} .{e}^{\mathrm{2}{t}} {log}\left({t}\right)}{{e}^{\mathrm{2}{t}} +{e}^{\mathrm{2}{t}−\mathrm{2}{t}} }=\frac{{e}^{{t}} {log}\left({t}\right)}{\mathrm{1}+{e}^{\mathrm{2}{t}} } \\ $$
