
Question Number 133183 by bounhome last updated on 19/Feb/21
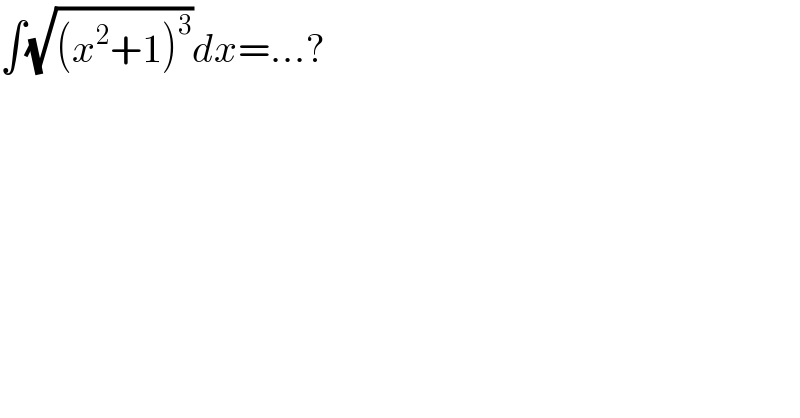
$$\int\sqrt{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }{dx}=...? \\ $$
Answered by physicstutes last updated on 19/Feb/21
![let x = sinh θ ⇒ dx = cosh θ dθ now, ∫(√([(sinh θ)^2 +1]^3 )) cosh θ dθ ⇒ ∫(√((cosh^2 θ)^3 )) cosh θ dθ = ∫(√(cosh^6 θ)) cosh θ dθ = ∫cosh^4 θ dθ I = ∫cosh^4 θdθ = (1/(32))(12θ + 8 sinh 2θ + sinh 4θ) + A, A ∈ R](Q133184.png)
$$\mathrm{let}\:{x}\:=\:\mathrm{sinh}\:\theta\:\Rightarrow\:{dx}\:=\:\mathrm{cosh}\:\theta\:{d}\theta \\ $$$$\mathrm{now},\:\int\sqrt{\left[\left(\mathrm{sinh}\:\theta\right)^{\mathrm{2}} +\mathrm{1}\right]^{\mathrm{3}} \:}\:\mathrm{cosh}\:\theta\:{d}\theta \\ $$$$\Rightarrow\:\int\sqrt{\left(\mathrm{cosh}^{\mathrm{2}} \theta\right)^{\mathrm{3}} }\:\mathrm{cosh}\:\theta\:{d}\theta\:=\:\int\sqrt{\mathrm{cosh}^{\mathrm{6}} \theta}\:\mathrm{cosh}\:\theta\:{d}\theta\:=\:\int\mathrm{cosh}^{\mathrm{4}} \theta\:{d}\theta \\ $$$$\mathcal{I}\:=\:\int\mathrm{cosh}^{\mathrm{4}} \theta{d}\theta\:\:=\:\frac{\mathrm{1}}{\mathrm{32}}\left(\mathrm{12}\theta\:+\:\mathrm{8}\:\mathrm{sinh}\:\mathrm{2}\theta\:+\:\mathrm{sinh}\:\mathrm{4}\theta\right)\:+\:{A},\:{A}\:\in\:\mathbb{R} \\ $$
Commented by Dwaipayan Shikari last updated on 19/Feb/21
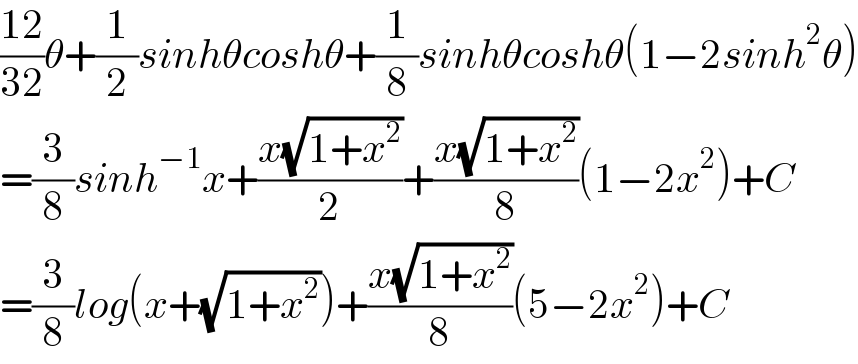
$$\frac{\mathrm{12}}{\mathrm{32}}\theta+\frac{\mathrm{1}}{\mathrm{2}}{sinh}\theta{cosh}\theta+\frac{\mathrm{1}}{\mathrm{8}}{sinh}\theta{cosh}\theta\left(\mathrm{1}−\mathrm{2}{sinh}^{\mathrm{2}} \theta\right) \\ $$$$=\frac{\mathrm{3}}{\mathrm{8}}{sinh}^{−\mathrm{1}} {x}+\frac{{x}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{\mathrm{2}}+\frac{{x}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{\mathrm{8}}\left(\mathrm{1}−\mathrm{2}{x}^{\mathrm{2}} \right)+{C} \\ $$$$=\frac{\mathrm{3}}{\mathrm{8}}{log}\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)+\frac{{x}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{\mathrm{8}}\left(\mathrm{5}−\mathrm{2}{x}^{\mathrm{2}} \right)+{C} \\ $$
