
Question Number 133114 by bemath last updated on 19/Feb/21
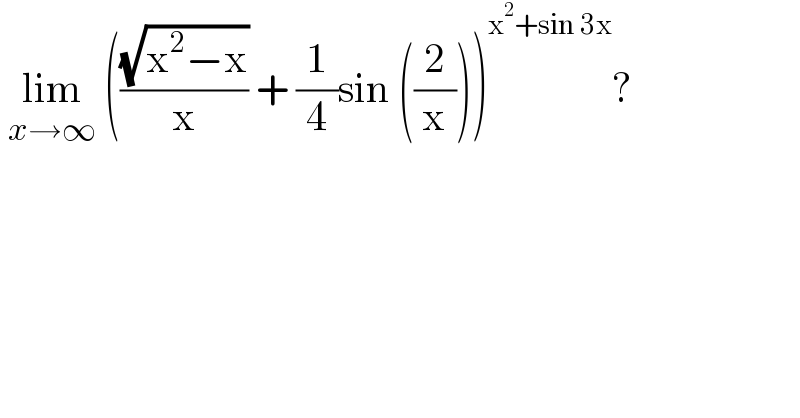
$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{x}}}{\mathrm{x}}\:+\:\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\:\left(\frac{\mathrm{2}}{\mathrm{x}}\right)\right)^{\mathrm{x}^{\mathrm{2}} +\mathrm{sin}\:\mathrm{3x}} ? \\ $$
Answered by bobhans last updated on 19/Feb/21

$${L}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\sqrt{{x}^{\mathrm{2}} −{x}}}{{x}}\:+\:\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\:\left(\frac{\mathrm{2}}{{x}}\right)\right)^{{x}^{\mathrm{2}} +\mathrm{sin}\:\left(\mathrm{3}{x}\right)} \\ $$$$=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\sqrt{\mathrm{1}−\frac{\mathrm{1}}{{x}}}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\:\left(\frac{\mathrm{2}}{{x}}\right)\right)^{{x}^{\mathrm{2}} +\mathrm{sin}\:\left(\mathrm{3}{x}\right)} \\ $$$$\mathrm{let}\:\frac{\mathrm{1}}{{x}}\:=\:{z}\:,\:{z}\rightarrow\mathrm{0}^{+} \\ $$$$=\underset{{z}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\left(\sqrt{\mathrm{1}−{z}}\:+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\:\left(\mathrm{2}{z}\right)\right)^{\frac{\mathrm{1}}{{z}^{\mathrm{2}} }+\mathrm{sin}\:\left(\frac{\mathrm{3}}{{z}}\right)} \\ $$$$\mathrm{ln}\:{L}\:=\:\underset{{z}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\left(\frac{\mathrm{1}}{{z}^{\mathrm{2}} }+\mathrm{sin}\:\left(\frac{\mathrm{3}}{{z}}\right)\right)\mathrm{ln}\:\left(\sqrt{\mathrm{1}−{z}}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\:\left(\mathrm{2}{z}\right)\right) \\ $$$$=\:\underset{{z}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\left(\frac{\left(\mathrm{1}+{z}^{\mathrm{2}} \mathrm{sin}\:\left(\frac{\mathrm{3}}{{z}}\right)\right)\mathrm{ln}\:\left(\sqrt{\mathrm{1}−{z}}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\:\mathrm{2}{z}\right)}{{z}^{\mathrm{2}} }\right. \\ $$$${by}\:{Sandwich}\:{theorem}\:{we}\:{get}\:{that}\: \\ $$$$\underset{{z}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\left(\mathrm{1}+{z}^{\mathrm{2}} \mathrm{sin}\:\left(\frac{\mathrm{3}}{{z}}\right)\right)=\:\mathrm{1} \\ $$$${therefore}\:{the}\:{limit}\:{reduces}\:{to} \\ $$$$\mathrm{ln}\:{L}=\:\underset{{z}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{\mathrm{ln}\:\left(\sqrt{\mathrm{1}−{z}}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\:\left(\mathrm{2}{z}\right)\right)}{{z}^{\mathrm{2}} } \\ $$$$\mathrm{ln}\:{L}=\:\underset{{z}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−{z}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} +\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\left(\mathrm{2}{t}\right)}{\mathrm{2}{t}\left(\sqrt{\mathrm{1}−{z}}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\:\mathrm{2}{z}\right)} \\ $$$$=\:\underset{{z}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{z}}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\:\mathrm{2}{z}}.\:\underset{{z}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{−\left(\mathrm{1}−{z}\right)^{−\mathrm{1}/\mathrm{2}} +\mathrm{cos}\:\mathrm{2}{z}}{\mathrm{4}{z}} \\ $$$$=\:\mathrm{1}\:.\underset{{z}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−{z}\right)^{−\mathrm{3}/\mathrm{2}} −\mathrm{2sin}\:\mathrm{2}{z}}{\mathrm{4}} \\ $$$$=\:−\frac{\mathrm{1}}{\mathrm{8}}\:;\:\mathrm{ln}\:{L}\:=\:−\frac{\mathrm{1}}{\mathrm{8}}\:{then}\:{L}\:=\:{e}^{−\mathrm{1}/\mathrm{8}} \\ $$$${or}\:{L}\:=\:\frac{\mathrm{1}}{\:\sqrt[{\mathrm{8}\:}]{{e}\:}}\: \\ $$
