
Question Number 133103 by 777316 last updated on 18/Feb/21

Commented by bemath last updated on 18/Feb/21
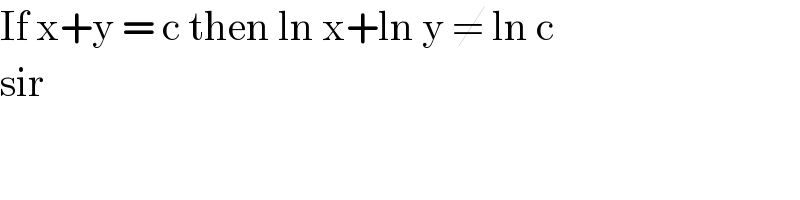
$$\mathrm{If}\:\mathrm{x}+\mathrm{y}\:=\:\mathrm{c}\:\mathrm{then}\:\mathrm{ln}\:\mathrm{x}+\mathrm{ln}\:\mathrm{y}\:\neq\:\mathrm{ln}\:\mathrm{c}\: \\ $$$$\mathrm{sir}\: \\ $$
Commented by malwan last updated on 18/Feb/21

$${yes} \\ $$$${you}\:{are}\:{right} \\ $$$${thank}\:{you} \\ $$
Answered by mr W last updated on 19/Feb/21
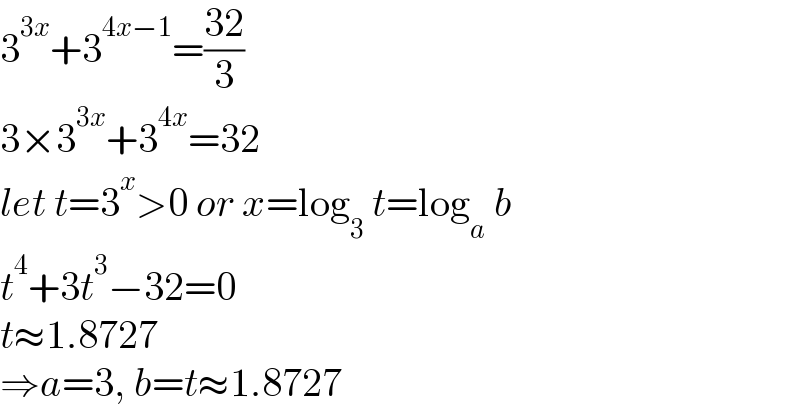
$$\mathrm{3}^{\mathrm{3}{x}} +\mathrm{3}^{\mathrm{4}{x}−\mathrm{1}} =\frac{\mathrm{32}}{\mathrm{3}} \\ $$$$\mathrm{3}×\mathrm{3}^{\mathrm{3}{x}} +\mathrm{3}^{\mathrm{4}{x}} =\mathrm{32} \\ $$$${let}\:{t}=\mathrm{3}^{{x}} >\mathrm{0}\:{or}\:{x}=\mathrm{log}_{\mathrm{3}} \:{t}=\mathrm{log}_{{a}} \:{b} \\ $$$${t}^{\mathrm{4}} +\mathrm{3}{t}^{\mathrm{3}} −\mathrm{32}=\mathrm{0} \\ $$$${t}\approx\mathrm{1}.\mathrm{8727} \\ $$$$\Rightarrow{a}=\mathrm{3},\:{b}={t}\approx\mathrm{1}.\mathrm{8727} \\ $$
Commented by otchereabdullai@gmail.com last updated on 19/Feb/21

$$\mathrm{nice}\:\mathrm{one} \\ $$
