
Question Number 132877 by mnjuly1970 last updated on 17/Feb/21
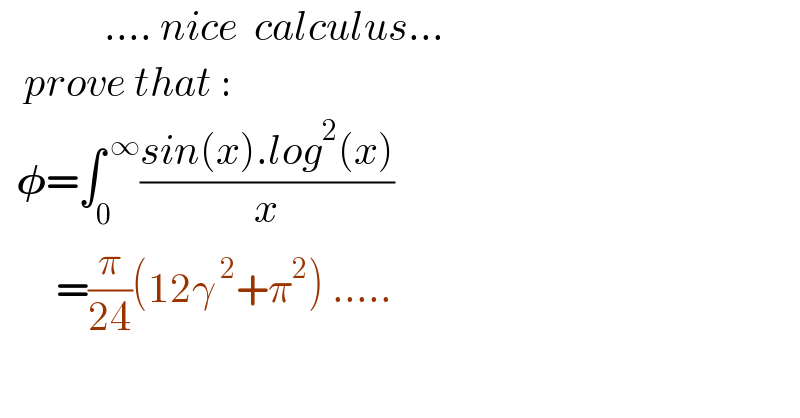
$$\:\:\:\:\:\:\:\:\:\:\:\:\:....\:{nice}\:\:{calculus}... \\ $$$$\:\:\:{prove}\:{that}\:: \\ $$$$\:\:\boldsymbol{\phi}=\int_{\mathrm{0}} ^{\:\infty} \frac{{sin}\left({x}\right).{log}^{\mathrm{2}} \left({x}\right)}{{x}} \\ $$$$\:\:\:\:\:\:\:=\frac{\pi}{\mathrm{24}}\left(\mathrm{12}\gamma^{\:\mathrm{2}} +\pi^{\mathrm{2}} \right)\:..... \\ $$
Answered by Dwaipayan Shikari last updated on 17/Feb/21
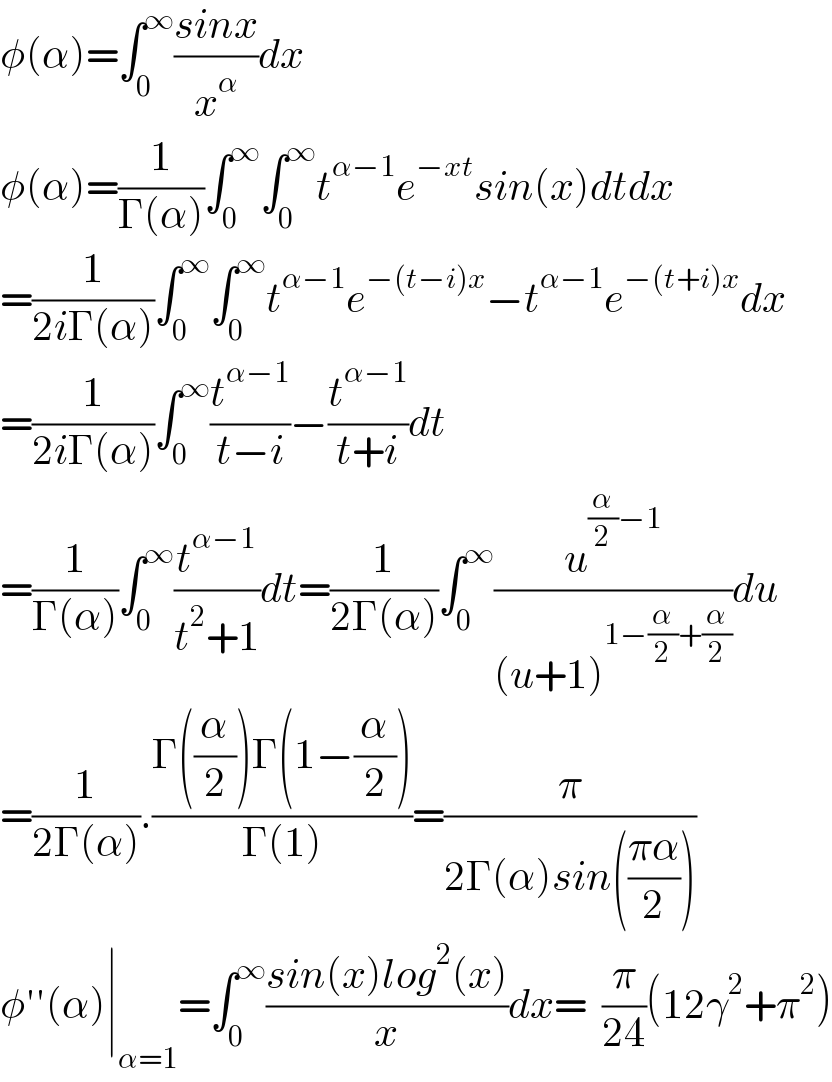
$$\phi\left(\alpha\right)=\int_{\mathrm{0}} ^{\infty} \frac{{sinx}}{{x}^{\alpha} }{dx} \\ $$$$\phi\left(\alpha\right)=\frac{\mathrm{1}}{\Gamma\left(\alpha\right)}\int_{\mathrm{0}} ^{\infty} \int_{\mathrm{0}} ^{\infty} {t}^{\alpha−\mathrm{1}} {e}^{−{xt}} {sin}\left({x}\right){dtdx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}\Gamma\left(\alpha\right)}\int_{\mathrm{0}} ^{\infty} \int_{\mathrm{0}} ^{\infty} {t}^{\alpha−\mathrm{1}} {e}^{−\left({t}−{i}\right){x}} −{t}^{\alpha−\mathrm{1}} {e}^{−\left({t}+{i}\right){x}} {dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}\Gamma\left(\alpha\right)}\int_{\mathrm{0}} ^{\infty} \frac{{t}^{\alpha−\mathrm{1}} }{{t}−{i}}−\frac{{t}^{\alpha−\mathrm{1}} }{{t}+{i}}{dt} \\ $$$$=\frac{\mathrm{1}}{\Gamma\left(\alpha\right)}\int_{\mathrm{0}} ^{\infty} \frac{{t}^{\alpha−\mathrm{1}} }{{t}^{\mathrm{2}} +\mathrm{1}}{dt}=\frac{\mathrm{1}}{\mathrm{2}\Gamma\left(\alpha\right)}\int_{\mathrm{0}} ^{\infty} \frac{{u}^{\frac{\alpha}{\mathrm{2}}−\mathrm{1}} }{\left({u}+\mathrm{1}\right)^{\mathrm{1}−\frac{\alpha}{\mathrm{2}}+\frac{\alpha}{\mathrm{2}}} }{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\Gamma\left(\alpha\right)}.\frac{\Gamma\left(\frac{\alpha}{\mathrm{2}}\right)\Gamma\left(\mathrm{1}−\frac{\alpha}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{1}\right)}=\frac{\pi}{\mathrm{2}\Gamma\left(\alpha\right){sin}\left(\frac{\pi\alpha}{\mathrm{2}}\right)} \\ $$$$\phi''\left(\alpha\right)\mid_{\alpha=\mathrm{1}} =\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left({x}\right){log}^{\mathrm{2}} \left({x}\right)}{{x}}{dx}=\:\:\frac{\pi}{\mathrm{24}}\left(\mathrm{12}\gamma^{\mathrm{2}} +\pi^{\mathrm{2}} \right) \\ $$
Commented by Dwaipayan Shikari last updated on 17/Feb/21
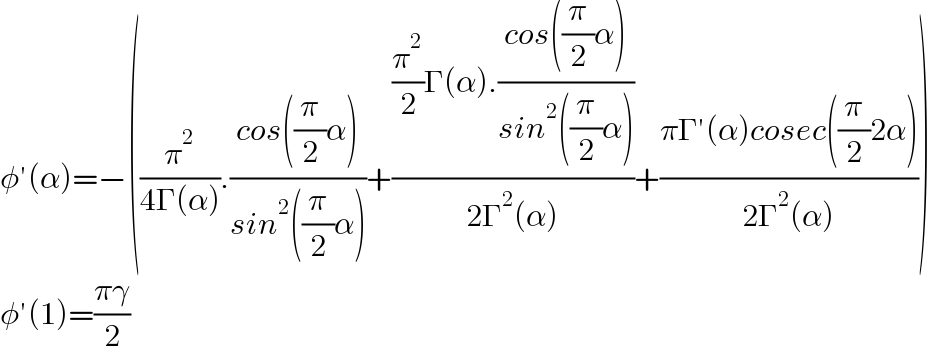
$$\phi'\left(\alpha\right)=−\left(\frac{\pi^{\mathrm{2}} }{\mathrm{4}\Gamma\left(\alpha\right)}.\frac{{cos}\left(\frac{\pi}{\mathrm{2}}\alpha\right)}{{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}}\alpha\right)}+\frac{\frac{\pi^{\mathrm{2}} }{\mathrm{2}}\Gamma\left(\alpha\right).\frac{{cos}\left(\frac{\pi}{\mathrm{2}}\alpha\right)}{{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}}\alpha\right)}}{\mathrm{2}\Gamma^{\mathrm{2}} \left(\alpha\right)}+\frac{\pi\Gamma'\left(\alpha\right){cosec}\left(\frac{\pi}{\mathrm{2}}\mathrm{2}\alpha\right)}{\mathrm{2}\Gamma^{\mathrm{2}} \left(\alpha\right)}\right) \\ $$$$\phi'\left(\mathrm{1}\right)=\frac{\pi\gamma}{\mathrm{2}} \\ $$
Commented by mnjuly1970 last updated on 17/Feb/21

$${with}\:{thanking}\:{sir}\:{payan}... \\ $$$$ \\ $$
