
Question Number 38516 by rahul 19 last updated on 26/Jun/18
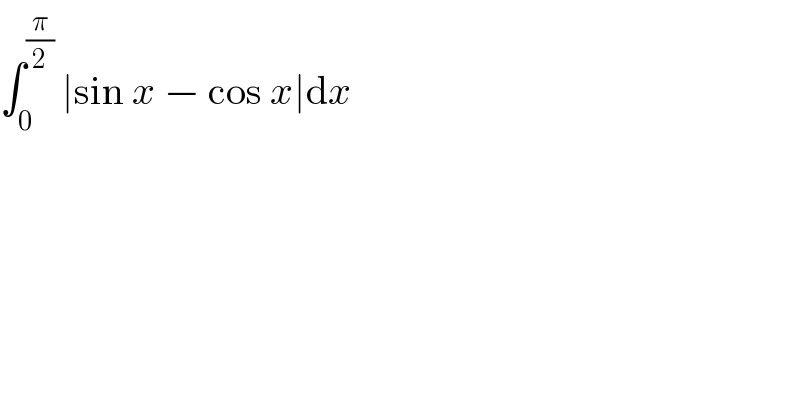
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mid\mathrm{sin}\:{x}\:−\:\mathrm{cos}\:{x}\mid\mathrm{d}{x} \\ $$
Commented by math khazana by abdo last updated on 27/Jun/18
![we have cosx −sinx=(√2)cos(x+(π/4)) ⇒ I =∫_0 ^(π/2) (√2)∣cos(x+(π/4))∣dx changement x+(π/4)=t give I =(√2)∫_(π/4) ^((3π)/4) ∣cost∣ dt =(√2){ ∫_(π/4) ^(π/2) cost dt + ∫_(π/2) ^((3π)/4) −cost dt} =(√2){ [sint]_(π/4) ^(π/2) −[sint]_(π/2) ^((3π)/4) } =(√2) { 1−((√2)/2) −(((√2)/2) −1)} =(√2){ 2−(√2)) = 2(√2) −2 = I =2(√2) −2](Q38540.png)
$${we}\:{have}\:{cosx}\:−{sinx}=\sqrt{\mathrm{2}}{cos}\left({x}+\frac{\pi}{\mathrm{4}}\right)\:\Rightarrow \\ $$$${I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{\mathrm{2}}\mid{cos}\left({x}+\frac{\pi}{\mathrm{4}}\right)\mid{dx}\:\:{changement} \\ $$$${x}+\frac{\pi}{\mathrm{4}}={t}\:{give}\:\:{I}\:=\sqrt{\mathrm{2}}\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\mathrm{3}\pi}{\mathrm{4}}} \:\mid{cost}\mid\:{dt} \\ $$$$=\sqrt{\mathrm{2}}\left\{\:\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \:{cost}\:{dt}\:+\:\int_{\frac{\pi}{\mathrm{2}}} ^{\frac{\mathrm{3}\pi}{\mathrm{4}}} \:−{cost}\:{dt}\right\} \\ $$$$=\sqrt{\mathrm{2}}\left\{\:\:\left[{sint}\right]_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \:\:−\left[{sint}\right]_{\frac{\pi}{\mathrm{2}}} ^{\frac{\mathrm{3}\pi}{\mathrm{4}}} \:\right\} \\ $$$$=\sqrt{\mathrm{2}}\:\left\{\:\:\mathrm{1}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:−\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:−\mathrm{1}\right)\right\} \\ $$$$=\sqrt{\mathrm{2}}\left\{\:\mathrm{2}−\sqrt{\mathrm{2}}\right)\:=\:\mathrm{2}\sqrt{\mathrm{2}}\:−\mathrm{2}\:= \\ $$$${I}\:=\mathrm{2}\sqrt{\mathrm{2}}\:−\mathrm{2} \\ $$
Answered by MJS last updated on 26/Jun/18
![sin x −cos x=−(√2)cos(x+(π/4)) cos(x+(π/4))=0 ⇒ x=(π/4) ∫_0 ^(π/2) ∣sin x −cos x∣dx= =(√2)∫_0 ^(π/4) cos(x+(π/4))dx−(√2)∫_(π/4) ^(π/2) cos(x+(π/4))dx= =2(√2)∫_0 ^(π/4) cos(x+(π/4))=2(√2)[sin(x+(π/4))]_0 ^(π/4) = =2(√2)−2](Q38524.png)
$$\mathrm{sin}\:{x}\:−\mathrm{cos}\:{x}=−\sqrt{\mathrm{2}}\mathrm{cos}\left({x}+\frac{\pi}{\mathrm{4}}\right) \\ $$$$\mathrm{cos}\left({x}+\frac{\pi}{\mathrm{4}}\right)=\mathrm{0}\:\Rightarrow\:{x}=\frac{\pi}{\mathrm{4}} \\ $$$$\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\mid\mathrm{sin}\:{x}\:−\mathrm{cos}\:{x}\mid{dx}= \\ $$$$=\sqrt{\mathrm{2}}\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{4}}} {\int}}\mathrm{cos}\left({x}+\frac{\pi}{\mathrm{4}}\right){dx}−\sqrt{\mathrm{2}}\underset{\frac{\pi}{\mathrm{4}}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\mathrm{cos}\left({x}+\frac{\pi}{\mathrm{4}}\right){dx}= \\ $$$$=\mathrm{2}\sqrt{\mathrm{2}}\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{4}}} {\int}}\mathrm{cos}\left({x}+\frac{\pi}{\mathrm{4}}\right)=\mathrm{2}\sqrt{\mathrm{2}}\left[\mathrm{sin}\left({x}+\frac{\pi}{\mathrm{4}}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} = \\ $$$$=\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 27/Jun/18
Answered by tanmay.chaudhury50@gmail.com last updated on 27/Jun/18
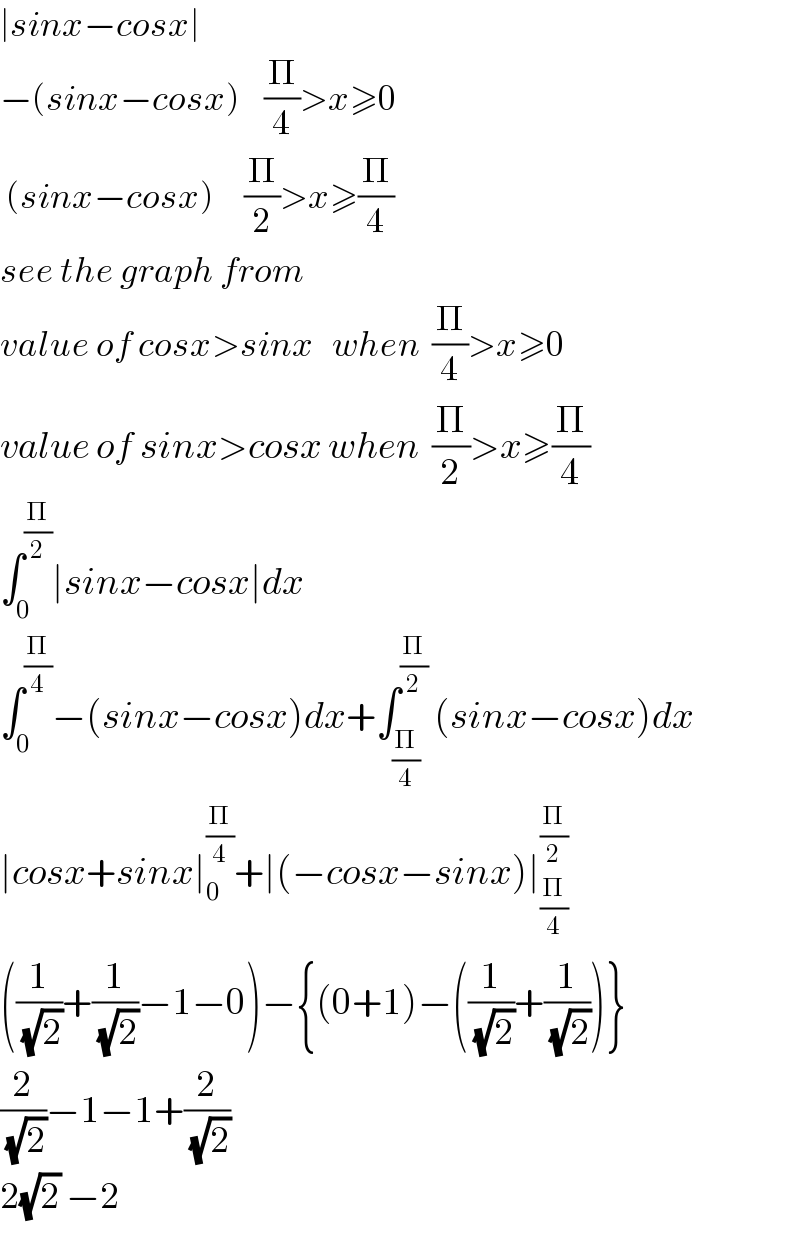
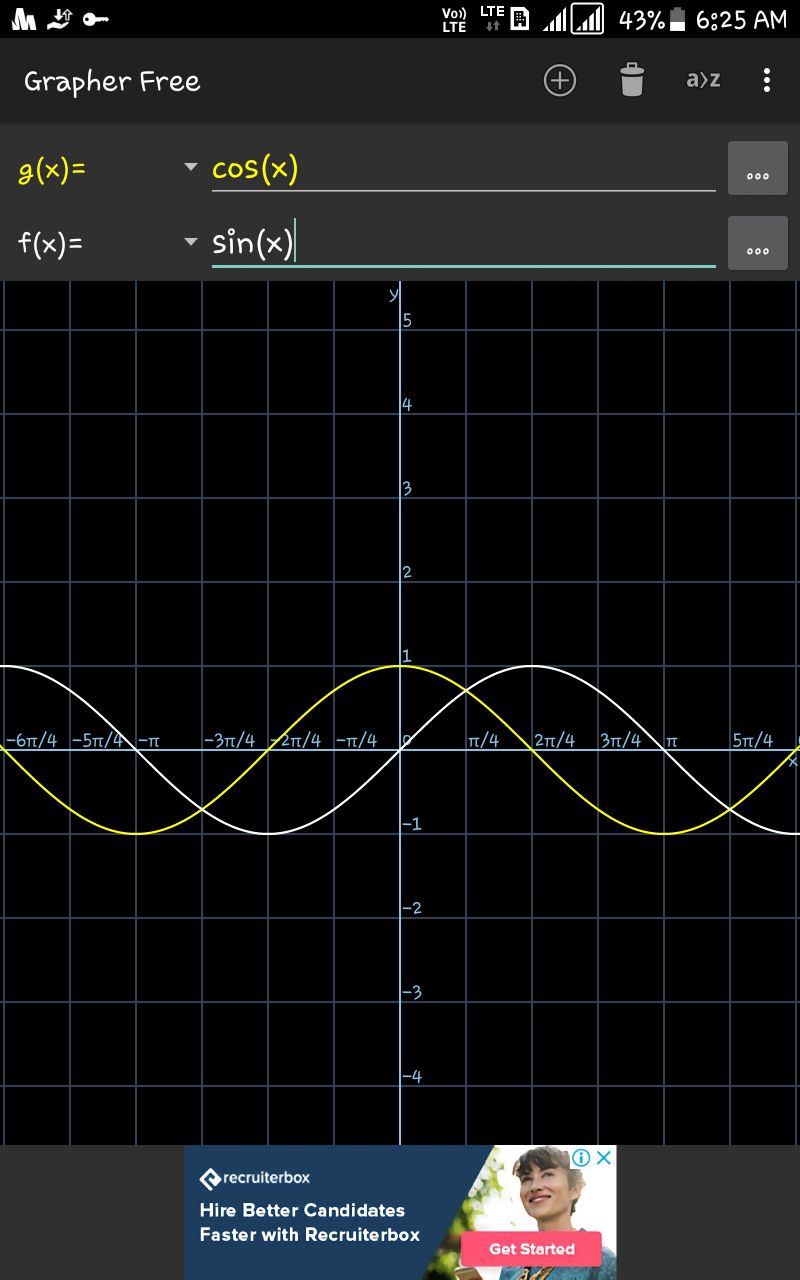
$$\mid{sinx}−{cosx}\mid \\ $$$$−\left({sinx}−{cosx}\right)\:\:\:\:\frac{\Pi}{\mathrm{4}}>{x}\geqslant\mathrm{0} \\ $$$$\:\left({sinx}−{cosx}\right)\:\:\:\:\:\frac{\Pi}{\mathrm{2}}>{x}\geqslant\frac{\Pi}{\mathrm{4}} \\ $$$${see}\:{the}\:{graph}\:{from}\: \\ $$$${value}\:{of}\:{cosx}>{sinx}\:\:\:{when}\:\:\frac{\Pi}{\mathrm{4}}>{x}\geqslant\mathrm{0} \\ $$$${value}\:{of}\:{sinx}>{cosx}\:{when}\:\:\frac{\Pi}{\mathrm{2}}>{x}\geqslant\frac{\Pi}{\mathrm{4}} \\ $$$$\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \mid{sinx}−{cosx}\mid{dx} \\ $$$$\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{4}}} −\left({sinx}−{cosx}\right){dx}+\int_{\frac{\Pi}{\mathrm{4}}} ^{\frac{\Pi}{\mathrm{2}}} \:\left({sinx}−{cosx}\right){dx} \\ $$$$\mid{cosx}+{sinx}\mid_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{4}}} +\mid\left(−{cosx}−{sinx}\right)\mid_{\frac{\Pi}{\mathrm{4}}} ^{\frac{\Pi}{\mathrm{2}}} \\ $$$$\left(\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}−\mathrm{1}−\mathrm{0}\right)−\left\{\left(\mathrm{0}+\mathrm{1}\right)−\left(\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\right)\right\} \\ $$$$\frac{\mathrm{2}}{\sqrt{\mathrm{2}}}−\mathrm{1}−\mathrm{1}+\frac{\mathrm{2}}{\sqrt{\mathrm{2}}} \\ $$$$\mathrm{2}\sqrt{\mathrm{2}}\:−\mathrm{2} \\ $$
