
Question Number 132785 by liberty last updated on 16/Feb/21

Commented by liberty last updated on 16/Feb/21
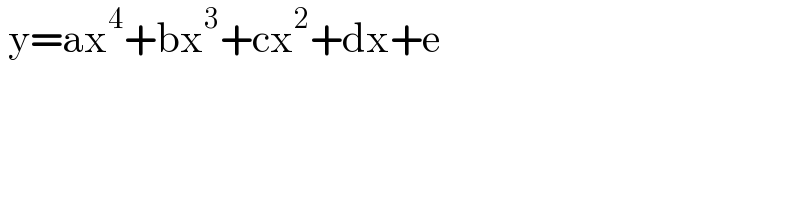
$$\:\mathrm{y}=\mathrm{ax}^{\mathrm{4}} +\mathrm{bx}^{\mathrm{3}} +\mathrm{cx}^{\mathrm{2}} +\mathrm{dx}+\mathrm{e} \\ $$
Answered by MJS_new last updated on 16/Feb/21
![“critical point” means min/max? in this case: p(x)=ax^4 +bx^3 +cx^2 +dx+e p′(x)=4ax^3 +3bx^2 +2cx+d p′′(x)=12ax^2 +6bx+2c we need 5 equations (1) p(0)=3 [(0∣3) on curve] (2) p′(0)=0 [min/max] (3) p(1)=2 [(1∣2) on curve] (4) p′′(1)=0 [inflection] (5) p′(1)=−6 [slope of tangent] now solve the system for a, b, c, d, e](Q132791.png)
$$``\mathrm{critical}\:\mathrm{point}''\:\mathrm{means}\:\mathrm{min}/\mathrm{max}?\:\mathrm{in}\:\mathrm{this}\:\mathrm{case}: \\ $$$${p}\left({x}\right)={ax}^{\mathrm{4}} +{bx}^{\mathrm{3}} +{cx}^{\mathrm{2}} +{dx}+{e} \\ $$$${p}'\left({x}\right)=\mathrm{4}{ax}^{\mathrm{3}} +\mathrm{3}{bx}^{\mathrm{2}} +\mathrm{2}{cx}+{d} \\ $$$${p}''\left({x}\right)=\mathrm{12}{ax}^{\mathrm{2}} +\mathrm{6}{bx}+\mathrm{2}{c} \\ $$$$\mathrm{we}\:\mathrm{need}\:\mathrm{5}\:\mathrm{equations} \\ $$$$\left(\mathrm{1}\right)\:{p}\left(\mathrm{0}\right)=\mathrm{3}\:\left[\left(\mathrm{0}\mid\mathrm{3}\right)\:\mathrm{on}\:\mathrm{curve}\right] \\ $$$$\left(\mathrm{2}\right)\:{p}'\left(\mathrm{0}\right)=\mathrm{0}\:\left[\mathrm{min}/\mathrm{max}\right] \\ $$$$\left(\mathrm{3}\right)\:{p}\left(\mathrm{1}\right)=\mathrm{2}\:\left[\left(\mathrm{1}\mid\mathrm{2}\right)\:\mathrm{on}\:\mathrm{curve}\right] \\ $$$$\left(\mathrm{4}\right)\:{p}''\left(\mathrm{1}\right)=\mathrm{0}\:\left[\mathrm{inflection}\right] \\ $$$$\left(\mathrm{5}\right)\:{p}'\left(\mathrm{1}\right)=−\mathrm{6}\:\left[\mathrm{slope}\:\mathrm{of}\:\mathrm{tangent}\right] \\ $$$$\mathrm{now}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{system}\:\mathrm{for}\:{a},\:{b},\:{c},\:{d},\:{e} \\ $$
Commented by liberty last updated on 16/Feb/21
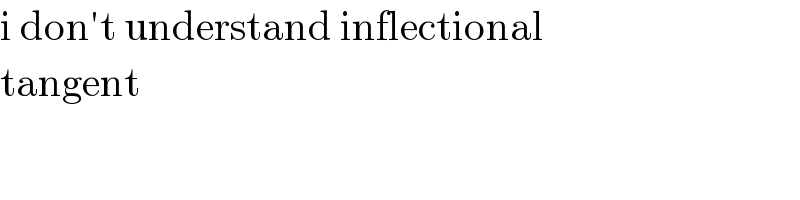
$$\mathrm{i}\:\mathrm{don}'\mathrm{t}\:\mathrm{understand}\:\mathrm{inflectional}\: \\ $$$$\mathrm{tangent} \\ $$
Commented by MJS_new last updated on 16/Feb/21
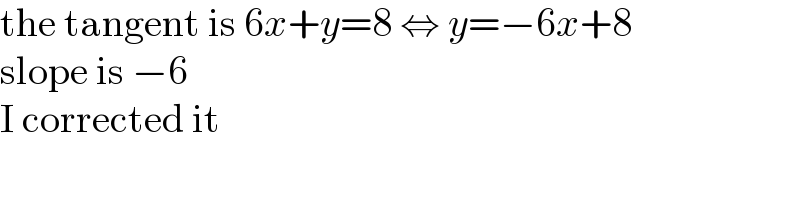
$$\mathrm{the}\:\mathrm{tangent}\:\mathrm{is}\:\mathrm{6}{x}+{y}=\mathrm{8}\:\Leftrightarrow\:{y}=−\mathrm{6}{x}+\mathrm{8} \\ $$$$\mathrm{slope}\:\mathrm{is}\:−\mathrm{6} \\ $$$$\mathrm{I}\:\mathrm{corrected}\:\mathrm{it} \\ $$
Commented by malwan last updated on 16/Feb/21
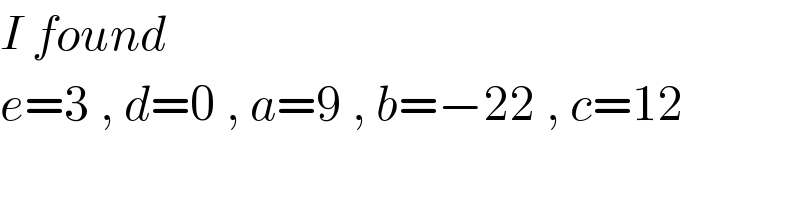
$${I}\:{found} \\ $$$${e}=\mathrm{3}\:,\:{d}=\mathrm{0}\:,\:{a}=\mathrm{9}\:,\:{b}=−\mathrm{22}\:,\:{c}=\mathrm{12} \\ $$
Commented by liberty last updated on 16/Feb/21

$$\mathrm{thank}\:\mathrm{you} \\ $$
