
Question Number 132762 by liberty last updated on 16/Feb/21

Answered by EDWIN88 last updated on 16/Feb/21
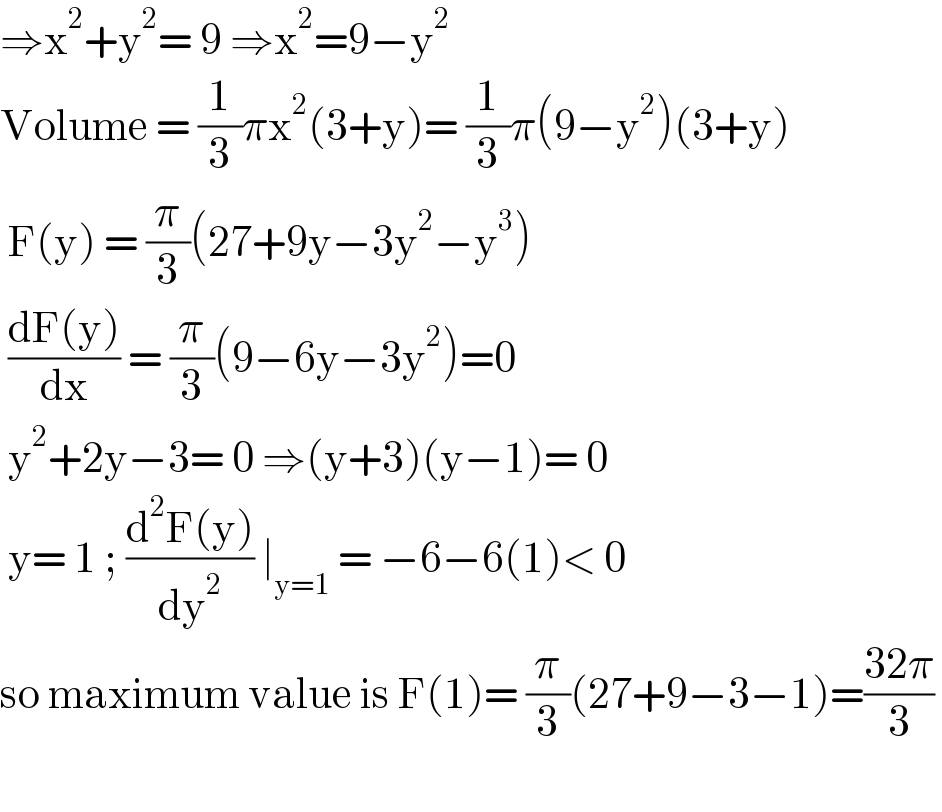
$$\Rightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} =\:\mathrm{9}\:\Rightarrow\mathrm{x}^{\mathrm{2}} =\mathrm{9}−\mathrm{y}^{\mathrm{2}} \\ $$$$\mathrm{Volume}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\pi\mathrm{x}^{\mathrm{2}} \left(\mathrm{3}+\mathrm{y}\right)=\:\frac{\mathrm{1}}{\mathrm{3}}\pi\left(\mathrm{9}−\mathrm{y}^{\mathrm{2}} \right)\left(\mathrm{3}+\mathrm{y}\right) \\ $$$$\:\mathrm{F}\left(\mathrm{y}\right)\:=\:\frac{\pi}{\mathrm{3}}\left(\mathrm{27}+\mathrm{9y}−\mathrm{3y}^{\mathrm{2}} −\mathrm{y}^{\mathrm{3}} \right)\: \\ $$$$\:\frac{\mathrm{dF}\left(\mathrm{y}\right)}{\mathrm{dx}}\:=\:\frac{\pi}{\mathrm{3}}\left(\mathrm{9}−\mathrm{6y}−\mathrm{3y}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\:\mathrm{y}^{\mathrm{2}} +\mathrm{2y}−\mathrm{3}=\:\mathrm{0}\:\Rightarrow\left(\mathrm{y}+\mathrm{3}\right)\left(\mathrm{y}−\mathrm{1}\right)=\:\mathrm{0} \\ $$$$\:\mathrm{y}=\:\mathrm{1}\:;\:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{F}\left(\mathrm{y}\right)}{\mathrm{dy}^{\mathrm{2}} }\:\mid_{\mathrm{y}=\mathrm{1}} \:=\:−\mathrm{6}−\mathrm{6}\left(\mathrm{1}\right)<\:\mathrm{0} \\ $$$$\mathrm{so}\:\mathrm{maximum}\:\mathrm{value}\:\mathrm{is}\:\mathrm{F}\left(\mathrm{1}\right)=\:\frac{\pi}{\mathrm{3}}\left(\mathrm{27}+\mathrm{9}−\mathrm{3}−\mathrm{1}\right)=\frac{\mathrm{32}\pi}{\mathrm{3}}\: \\ $$$$ \\ $$
Answered by Olaf last updated on 16/Feb/21
![x^2 +y^2 = 9 h = 3+y = 3+(√(9−x^2 )) V(x) = (1/3)πx^2 h = (π/3)x^2 (3+(√(9−x^2 ))) V′(x) = (π/3)[2x(3+(√(9−x^2 )))+x^2 (((−2x)/(2(√(9−x^2 )))))] V′(x) = ((πx)/3)[2(3+(√(9−x^2 )))−(x^2 /( (√(9−x^2 ))))] V′(x) = 0 ⇔ 6(√(9−x^2 ))+2(9−x^2 )−x^2 = 0 ⇔ 2(√(9−x^2 )) = x^2 −6 ⇔ 4(9−x^2 ) = (x^2 −6)^2 ⇔ x^4 −12x^2 +36+4x^2 −36 = 0 ⇔ x^2 (x^2 −8) = 0 maximum for x = 2(√2) V_(max) = V(2(√2)) = (π/3).8.(3+(√(9−8))) V_(max) = ((32π)/3)](Q132770.png)
$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} \:=\:\mathrm{9} \\ $$$${h}\:=\:\mathrm{3}+{y}\:=\:\mathrm{3}+\sqrt{\mathrm{9}−{x}^{\mathrm{2}} } \\ $$$$\mathrm{V}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{3}}\pi{x}^{\mathrm{2}} {h}\:=\:\frac{\pi}{\mathrm{3}}{x}^{\mathrm{2}} \left(\mathrm{3}+\sqrt{\mathrm{9}−{x}^{\mathrm{2}} }\right) \\ $$$$\mathrm{V}'\left({x}\right)\:=\:\frac{\pi}{\mathrm{3}}\left[\mathrm{2}{x}\left(\mathrm{3}+\sqrt{\mathrm{9}−{x}^{\mathrm{2}} }\right)+{x}^{\mathrm{2}} \left(\frac{−\mathrm{2}{x}}{\mathrm{2}\sqrt{\mathrm{9}−{x}^{\mathrm{2}} }}\right)\right] \\ $$$$\mathrm{V}'\left({x}\right)\:=\:\frac{\pi{x}}{\mathrm{3}}\left[\mathrm{2}\left(\mathrm{3}+\sqrt{\mathrm{9}−{x}^{\mathrm{2}} }\right)−\frac{{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{9}−{x}^{\mathrm{2}} }}\right] \\ $$$$\mathrm{V}'\left({x}\right)\:=\:\mathrm{0} \\ $$$$\Leftrightarrow\:\mathrm{6}\sqrt{\mathrm{9}−{x}^{\mathrm{2}} }+\mathrm{2}\left(\mathrm{9}−{x}^{\mathrm{2}} \right)−{x}^{\mathrm{2}} \:=\:\mathrm{0} \\ $$$$\Leftrightarrow\:\mathrm{2}\sqrt{\mathrm{9}−{x}^{\mathrm{2}} }\:=\:{x}^{\mathrm{2}} −\mathrm{6} \\ $$$$\Leftrightarrow\:\mathrm{4}\left(\mathrm{9}−{x}^{\mathrm{2}} \right)\:=\:\left({x}^{\mathrm{2}} −\mathrm{6}\right)^{\mathrm{2}} \\ $$$$\Leftrightarrow\:{x}^{\mathrm{4}} −\mathrm{12}{x}^{\mathrm{2}} +\mathrm{36}+\mathrm{4}{x}^{\mathrm{2}} −\mathrm{36}\:=\:\mathrm{0} \\ $$$$\Leftrightarrow\:{x}^{\mathrm{2}} \left({x}^{\mathrm{2}} −\mathrm{8}\right)\:=\:\mathrm{0} \\ $$$${maximum}\:{for}\:{x}\:=\:\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$\mathrm{V}_{{max}} \:=\:\mathrm{V}\left(\mathrm{2}\sqrt{\mathrm{2}}\right)\:=\:\frac{\pi}{\mathrm{3}}.\mathrm{8}.\left(\mathrm{3}+\sqrt{\mathrm{9}−\mathrm{8}}\right) \\ $$$$\mathrm{V}_{{max}} \:=\:\frac{\mathrm{32}\pi}{\mathrm{3}} \\ $$
Commented by otchereabdullai@gmail.com last updated on 14/Mar/21

$$\mathrm{nice}! \\ $$
