
Question Number 132755 by liberty last updated on 16/Feb/21
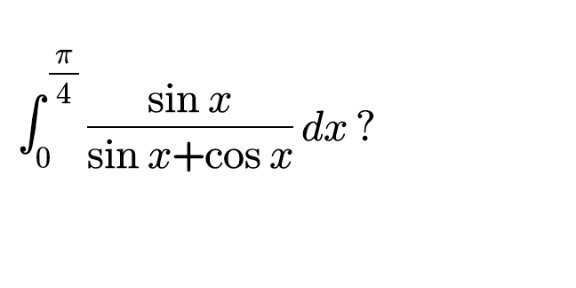
Commented by KINTU last updated on 16/Feb/21
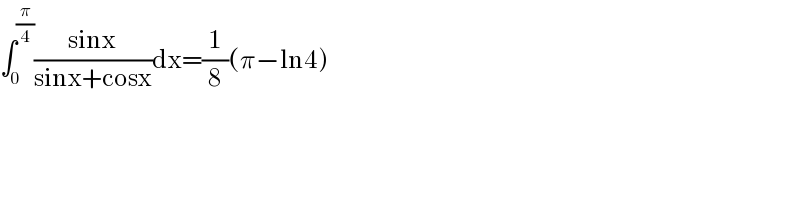
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\mathrm{sinx}}{\mathrm{sinx}+\mathrm{cosx}}\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{8}}\left(\pi−\mathrm{ln4}\right) \\ $$
Answered by EDWIN88 last updated on 16/Feb/21
![Let I= ∫_0 ^(π/4) ((sin x)/(sin x+cos x)) dx , J = ∫_0 ^( (π/4)) ((cos x)/(sin x+cos x)) dx We have I+J = ∫_0 ^(π/4) ((sin x+cos x)/(sin x+cos x)) dx = (π/4) and I−J = ∫_0 ^(π/4) ((sin x−cos x)/(sin x+cos x)) dx = −∫_0 ^(π/4) ((d(sin x+cos x))/(sin x+cos x)) = −ln ∣sin x+cos x∣_0 ^(π/4) = −ln (√2) We asked the value of I , we find it from I = (1/2) [(I+J)+(I−J) ] I=(1/2) [(π/4)−ln (√2) ] = (π/8)−(1/4)ln (2)](Q132756.png)
$$\:\mathrm{Let}\:\mathrm{I}=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{sin}\:{x}}{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}\:{dx}\:,\:\mathrm{J}\:=\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}\:{dx} \\ $$$$\mathrm{We}\:\mathrm{have}\:\mathrm{I}+\mathrm{J}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}\:{dx}\:=\:\frac{\pi}{\mathrm{4}} \\ $$$$\mathrm{and}\:\mathrm{I}−\mathrm{J}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{sin}\:{x}−\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}\:{dx}\:=\:−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{d}\left(\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}\right)}{\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}} \\ $$$$\:=\:−\mathrm{ln}\:\mid\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} =\:−\mathrm{ln}\:\sqrt{\mathrm{2}}\: \\ $$$$\mathrm{We}\:\mathrm{asked}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{I}\:,\:\mathrm{we}\:\mathrm{find}\:\mathrm{it}\:\mathrm{from} \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\left[\left(\mathrm{I}+\mathrm{J}\right)+\left(\mathrm{I}−\mathrm{J}\right)\:\right] \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\mathrm{2}}\:\left[\frac{\pi}{\mathrm{4}}−\mathrm{ln}\:\sqrt{\mathrm{2}}\:\right]\:=\:\frac{\pi}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\left(\mathrm{2}\right) \\ $$
Answered by MJS_new last updated on 16/Feb/21
![∫_0 ^(π/4) ((sin x)/(sin x +cos x))dx=∫_(π/4) ^(π/2) ((sin (x−(π/4)))/(sin (x−(π/4)) +cos (x−(π/4))))dx= =∫_(π/4) ^(π/2) ((−cos (x+(π/4)))/( (√2)sin x))dx=∫_(π/4) ^(π/2) ((((√2)/2)(sin x −cos x))/( (√2)sin x))dx= =(1/2)∫_(π/4) ^(π/2) (1−cot x)dx=(1/2)[x−ln ∣sin x∣]_(π/4) ^(π/2) = =(π/8)−((ln 2)/4)](Q132771.png)
$$\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}\frac{\mathrm{sin}\:{x}}{\mathrm{sin}\:{x}\:+\mathrm{cos}\:{x}}{dx}=\underset{\pi/\mathrm{4}} {\overset{\pi/\mathrm{2}} {\int}}\frac{\mathrm{sin}\:\left({x}−\frac{\pi}{\mathrm{4}}\right)}{\mathrm{sin}\:\left({x}−\frac{\pi}{\mathrm{4}}\right)\:+\mathrm{cos}\:\left({x}−\frac{\pi}{\mathrm{4}}\right)}{dx}= \\ $$$$=\underset{\pi/\mathrm{4}} {\overset{\pi/\mathrm{2}} {\int}}\frac{−\mathrm{cos}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)}{\:\sqrt{\mathrm{2}}\mathrm{sin}\:{x}}{dx}=\underset{\pi/\mathrm{4}} {\overset{\pi/\mathrm{2}} {\int}}\frac{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\mathrm{sin}\:{x}\:−\mathrm{cos}\:{x}\right)}{\:\sqrt{\mathrm{2}}\mathrm{sin}\:{x}}{dx}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{\pi/\mathrm{4}} {\overset{\pi/\mathrm{2}} {\int}}\left(\mathrm{1}−\mathrm{cot}\:{x}\right){dx}=\frac{\mathrm{1}}{\mathrm{2}}\left[{x}−\mathrm{ln}\:\mid\mathrm{sin}\:{x}\mid\right]_{\pi/\mathrm{4}} ^{\pi/\mathrm{2}} = \\ $$$$=\frac{\pi}{\mathrm{8}}−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{4}} \\ $$
Answered by malwan last updated on 16/Feb/21
![_0 ∫^( (π/4)) ((sinx +(−cosx+cosx)+(sinx−sinx))/(sinx+cosx))dx = −ln∣sinx+cosx∣+ x −∫((sinx)/(sinx+cosx))dx ⇒ _0 ∫^(π/4) ((sinx)/(sinx+cosx))dx= (1/2)[x−ln∣sinx+cosx∣]_0 ^(π/4) =(1/2)[((π/4) −ln(√2))−(0−ln(1))] =(π/8) − (1/2)ln2^(1/2) = (π/8) − (1/4)ln2](Q132787.png)
$$\:_{\mathrm{0}} \int^{\:\frac{\pi}{\mathrm{4}}} \frac{{sinx}\:+\left(−{cosx}+{cosx}\right)+\left({sinx}−{sinx}\right)}{{sinx}+{cosx}}{dx} \\ $$$$=\:−{ln}\mid{sinx}+{cosx}\mid+\:{x}\:−\int\frac{{sinx}}{{sinx}+{cosx}}{dx} \\ $$$$\Rightarrow\:_{\mathrm{0}} \int^{\frac{\pi}{\mathrm{4}}} \frac{{sinx}}{{sinx}+{cosx}}{dx}=\:\frac{\mathrm{1}}{\mathrm{2}}\left[{x}−{ln}\mid{sinx}+{cosx}\mid\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\left(\frac{\pi}{\mathrm{4}}\:−{ln}\sqrt{\mathrm{2}}\right)−\left(\mathrm{0}−{ln}\left(\mathrm{1}\right)\right)\right] \\ $$$$=\frac{\pi}{\mathrm{8}}\:−\:\frac{\mathrm{1}}{\mathrm{2}}{ln}\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{2}}} =\:\frac{\pi}{\mathrm{8}}\:−\:\frac{\mathrm{1}}{\mathrm{4}}{ln}\mathrm{2} \\ $$
