
Question Number 132741 by mnjuly1970 last updated on 16/Feb/21
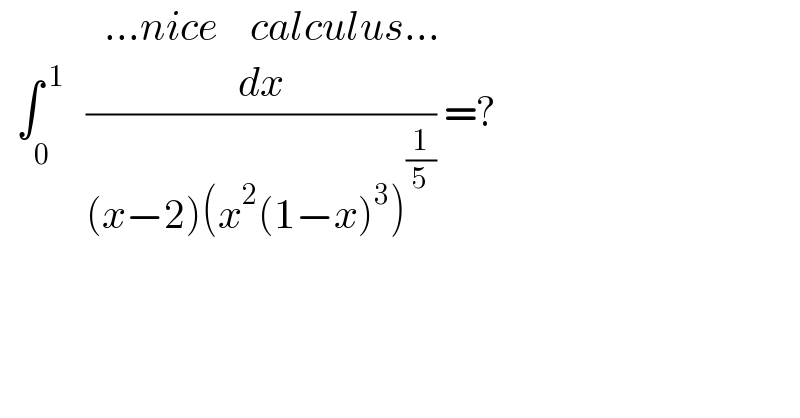
$$\:\:\:\:\:\:\:\:\:\:\:\:\:...{nice}\:\:\:\:{calculus}... \\ $$$$\:\:\int_{\mathrm{0}^{\:\:\:\:} \:\:} ^{\:\mathrm{1}} \frac{{dx}}{\left({x}−\mathrm{2}\right)\left({x}^{\mathrm{2}} \left(\mathrm{1}−{x}\right)^{\mathrm{3}} \right)^{\frac{\mathrm{1}}{\mathrm{5}}} }\:=? \\ $$
Commented by MJS_new last updated on 16/Feb/21
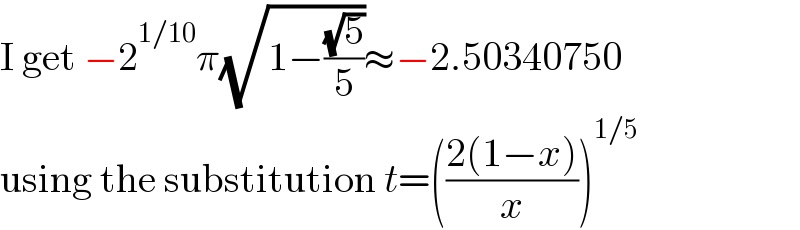
$$\mathrm{I}\:\mathrm{get}\:−\mathrm{2}^{\mathrm{1}/\mathrm{10}} \pi\sqrt{\mathrm{1}−\frac{\sqrt{\mathrm{5}}}{\mathrm{5}}}\approx−\mathrm{2}.\mathrm{50340750} \\ $$$$\mathrm{using}\:\mathrm{the}\:\mathrm{substitution}\:{t}=\left(\frac{\mathrm{2}\left(\mathrm{1}−{x}\right)}{{x}}\right)^{\mathrm{1}/\mathrm{5}} \\ $$
Commented by MJS_new last updated on 16/Feb/21
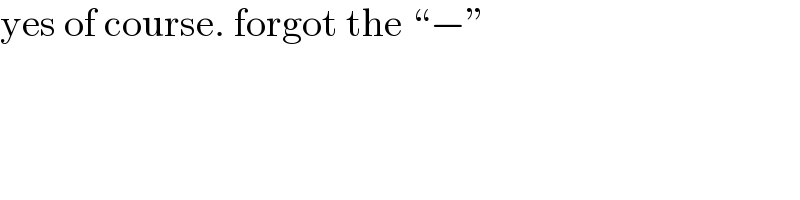
$$\mathrm{yes}\:\mathrm{of}\:\mathrm{course}.\:\mathrm{forgot}\:\mathrm{the}\:``−'' \\ $$
Commented by Dwaipayan Shikari last updated on 16/Feb/21
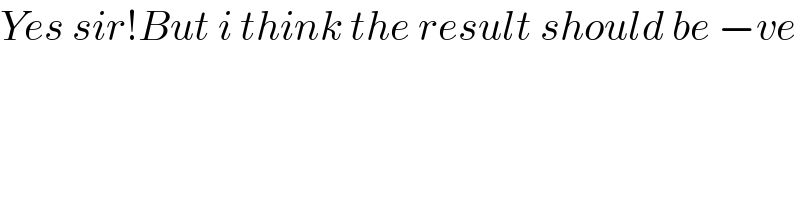
$${Yes}\:{sir}!{But}\:{i}\:{think}\:{the}\:{result}\:{should}\:{be}\:−{ve} \\ $$
Commented by mnjuly1970 last updated on 16/Feb/21
$${bravo}\:\:{mr}\:{Mj} \\ $$$${thank}\:{you}\:{so}\:{much}... \\ $$
Answered by Dwaipayan Shikari last updated on 16/Feb/21
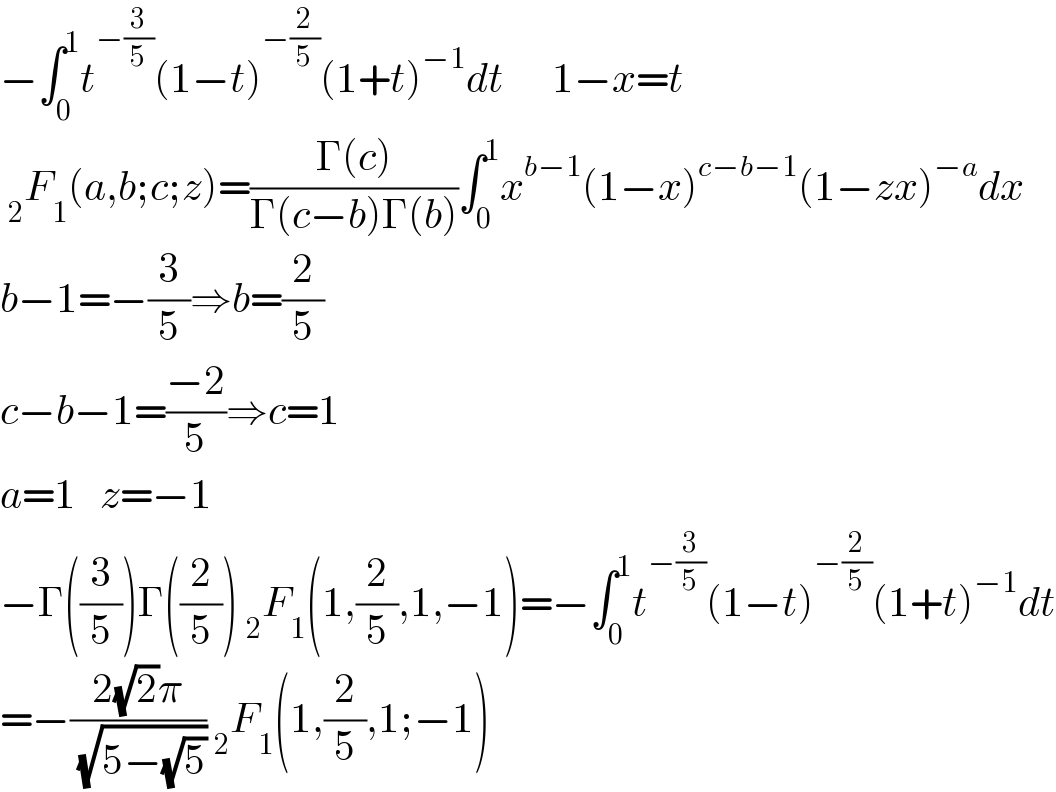
$$−\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{−\frac{\mathrm{3}}{\mathrm{5}}} \left(\mathrm{1}−{t}\right)^{−\frac{\mathrm{2}}{\mathrm{5}}} \left(\mathrm{1}+{t}\right)^{−\mathrm{1}} {dt}\:\:\:\:\:\:\mathrm{1}−{x}={t} \\ $$$$\:_{\mathrm{2}} {F}_{\mathrm{1}} \left({a},{b};{c};{z}\right)=\frac{\Gamma\left({c}\right)}{\Gamma\left({c}−{b}\right)\Gamma\left({b}\right)}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{b}−\mathrm{1}} \left(\mathrm{1}−{x}\right)^{{c}−{b}−\mathrm{1}} \left(\mathrm{1}−{zx}\right)^{−{a}} {dx} \\ $$$${b}−\mathrm{1}=−\frac{\mathrm{3}}{\mathrm{5}}\Rightarrow{b}=\frac{\mathrm{2}}{\mathrm{5}} \\ $$$${c}−{b}−\mathrm{1}=\frac{−\mathrm{2}}{\mathrm{5}}\Rightarrow{c}=\mathrm{1} \\ $$$${a}=\mathrm{1}\:\:\:{z}=−\mathrm{1} \\ $$$$−\Gamma\left(\frac{\mathrm{3}}{\mathrm{5}}\right)\Gamma\left(\frac{\mathrm{2}}{\mathrm{5}}\right)\:_{\mathrm{2}} {F}_{\mathrm{1}} \left(\mathrm{1},\frac{\mathrm{2}}{\mathrm{5}},\mathrm{1},−\mathrm{1}\right)=−\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{−\frac{\mathrm{3}}{\mathrm{5}}} \left(\mathrm{1}−{t}\right)^{−\frac{\mathrm{2}}{\mathrm{5}}} \left(\mathrm{1}+{t}\right)^{−\mathrm{1}} {dt} \\ $$$$=−\frac{\mathrm{2}\sqrt{\mathrm{2}}\pi}{\:\sqrt{\mathrm{5}−\sqrt{\mathrm{5}}}}\:_{\mathrm{2}} {F}_{\mathrm{1}} \left(\mathrm{1},\frac{\mathrm{2}}{\mathrm{5}},\mathrm{1};−\mathrm{1}\right) \\ $$
Commented by mnjuly1970 last updated on 16/Feb/21
$${mercey}\: \\ $$$${grateful}... \\ $$$$\:{hypergeometrey}\:{function}... \\ $$
