Question Number 132407 by bramlexs22 last updated on 14/Feb/21
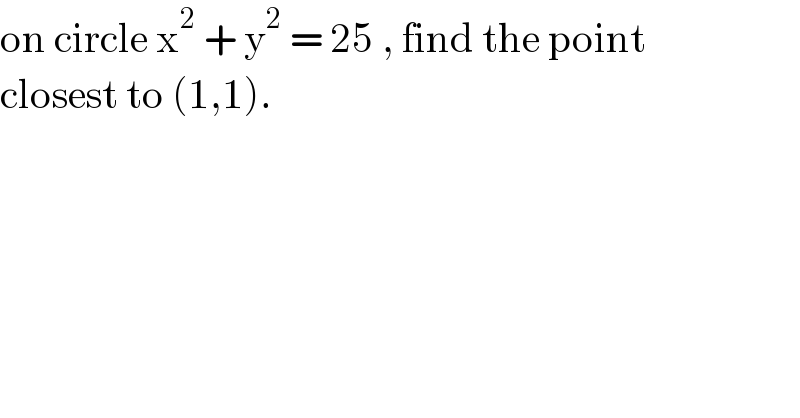
$$\mathrm{on}\:\mathrm{circle}\:\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{y}^{\mathrm{2}} \:=\:\mathrm{25}\:,\:\mathrm{find}\:\mathrm{the}\:\mathrm{point} \\ $$$$\mathrm{closest}\:\mathrm{to}\:\left(\mathrm{1},\mathrm{1}\right). \\ $$
Answered by EDWIN88 last updated on 14/Feb/21

$$\mathrm{let}\:\mathrm{P}\left(\mathrm{x},\mathrm{y}\right)\:\mathrm{be}\:\mathrm{a}\:\mathrm{point}\:\mathrm{on}\:\mathrm{a}\:\mathrm{circle}\: \\ $$$$\mathrm{let}\:\mathrm{x}\:\mathrm{be}\:\mathrm{a}\:\mathrm{distance}\:\mathrm{of}\:\mathrm{plint}\:\left(\mathrm{1},\mathrm{1}\right)\:\mathrm{to}\:\left(\mathrm{x},\mathrm{y}\right) \\ $$$$\mathrm{d}^{\mathrm{2}} =\:\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{y}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\mathrm{d}^{\mathrm{2}} =\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{25}−\mathrm{x}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{25}−\mathrm{x}^{\mathrm{2}} }\:+\mathrm{1} \\ $$$$\mathrm{d}^{\mathrm{2}} =\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{1}+\mathrm{25}−\mathrm{x}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{25}−\mathrm{x}^{\mathrm{2}} }\:+\mathrm{1} \\ $$$$\mathrm{d}^{\mathrm{2}} =\:\mathrm{27}−\mathrm{2x}−\mathrm{2}\sqrt{\mathrm{25}−\mathrm{x}^{\mathrm{2}} }\: \\ $$$$\mathrm{differentiating}\:\mathrm{w}.\mathrm{r}.\mathrm{t}\:\mathrm{x} \\ $$$$\left(\mathrm{d}^{\mathrm{2}} \right)'=\:−\mathrm{2}−\mathrm{2}\left(\frac{−\mathrm{x}}{\:\sqrt{\mathrm{25}−\mathrm{x}^{\mathrm{2}} }}\:\right)=\mathrm{0} \\ $$$$\:\frac{\mathrm{x}}{\:\sqrt{\mathrm{25}−\mathrm{x}^{\mathrm{2}} }}\:=\:\mathrm{1}\Leftrightarrow\mathrm{2x}^{\mathrm{2}} =\mathrm{25}\:\Rightarrow\mathrm{x}=\pm\frac{\mathrm{5}}{\:\sqrt{\mathrm{2}}} \\ $$$$\mathrm{and}\:\mathrm{y}\:=\:\pm\:\sqrt{\mathrm{25}−\frac{\mathrm{25}}{\mathrm{2}}}\:=\:\pm\frac{\mathrm{5}}{\:\sqrt{\mathrm{2}}}\:\mathrm{the}\:\mathrm{point} \\ $$$$\mathrm{on}\:\mathrm{circle}\:\mathrm{such}\:\mathrm{that}\:\mathrm{closest}\:\mathrm{to}\:\left(\mathrm{1},\mathrm{1}\right)\:\mathrm{is}\:\left(\frac{\mathrm{5}}{\:\sqrt{\mathrm{2}}}\:,\:\frac{\mathrm{5}}{\:\sqrt{\mathrm{2}}}\:\right) \\ $$
Commented by EDWIN88 last updated on 14/Feb/21