
Question Number 132368 by otchereabdullai@gmail.com last updated on 13/Feb/21
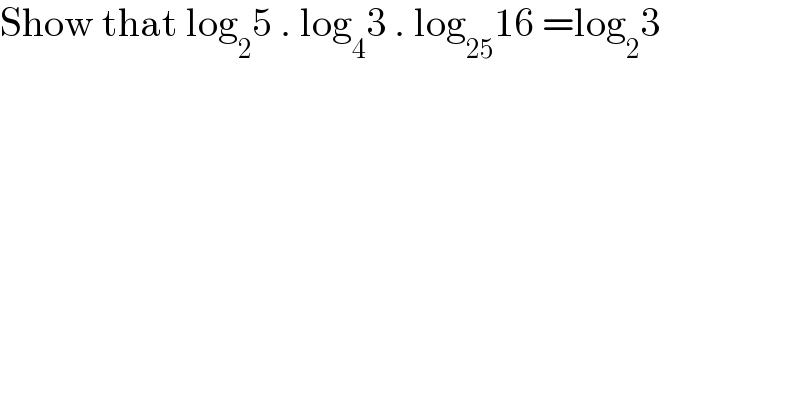
$$\mathrm{Show}\:\mathrm{that}\:\mathrm{log}_{\mathrm{2}} \mathrm{5}\:.\:\mathrm{log}_{\mathrm{4}} \mathrm{3}\:.\:\mathrm{log}_{\mathrm{25}} \mathrm{16}\:=\mathrm{log}_{\mathrm{2}} \mathrm{3} \\ $$
Answered by mr W last updated on 13/Feb/21
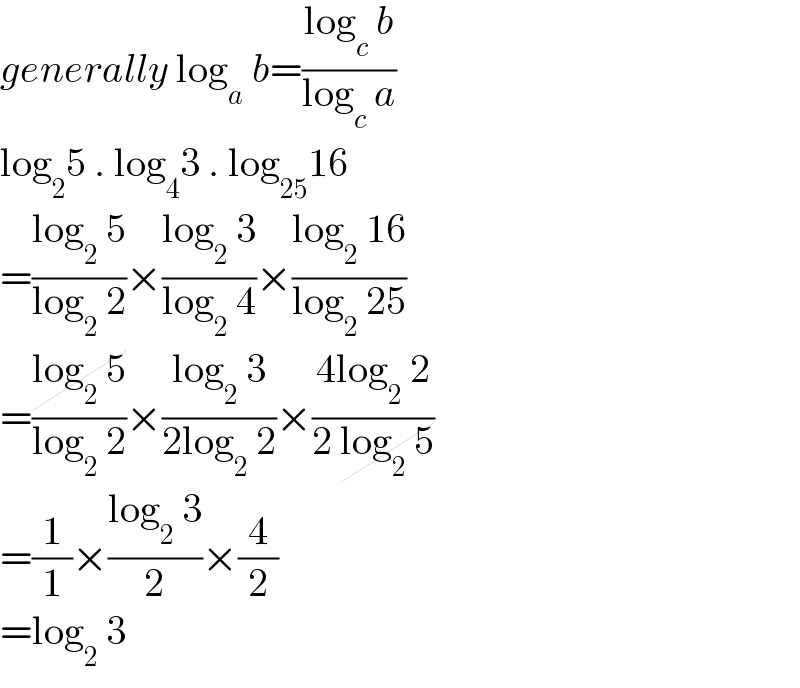
$${generally}\:\mathrm{log}_{{a}} \:{b}=\frac{\mathrm{log}_{{c}} \:{b}}{\mathrm{log}_{{c}} \:{a}} \\ $$$$\mathrm{log}_{\mathrm{2}} \mathrm{5}\:.\:\mathrm{log}_{\mathrm{4}} \mathrm{3}\:.\:\mathrm{log}_{\mathrm{25}} \mathrm{16} \\ $$$$=\frac{\mathrm{log}_{\mathrm{2}} \:\mathrm{5}}{\mathrm{log}_{\mathrm{2}} \:\mathrm{2}}×\frac{\mathrm{log}_{\mathrm{2}} \:\mathrm{3}}{\mathrm{log}_{\mathrm{2}} \:\mathrm{4}}×\frac{\mathrm{log}_{\mathrm{2}} \:\mathrm{16}}{\mathrm{log}_{\mathrm{2}} \:\mathrm{25}} \\ $$$$=\frac{\cancel{\mathrm{log}_{\mathrm{2}} \:\mathrm{5}}}{\mathrm{log}_{\mathrm{2}} \:\mathrm{2}}×\frac{\mathrm{log}_{\mathrm{2}} \:\mathrm{3}}{\mathrm{2log}_{\mathrm{2}} \:\mathrm{2}}×\frac{\mathrm{4log}_{\mathrm{2}} \:\mathrm{2}}{\mathrm{2}\:\cancel{\mathrm{log}_{\mathrm{2}} \:\mathrm{5}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}}×\frac{\mathrm{log}_{\mathrm{2}} \:\mathrm{3}}{\mathrm{2}}×\frac{\mathrm{4}}{\mathrm{2}} \\ $$$$=\mathrm{log}_{\mathrm{2}} \:\mathrm{3} \\ $$
Commented by otchereabdullai@gmail.com last updated on 13/Feb/21
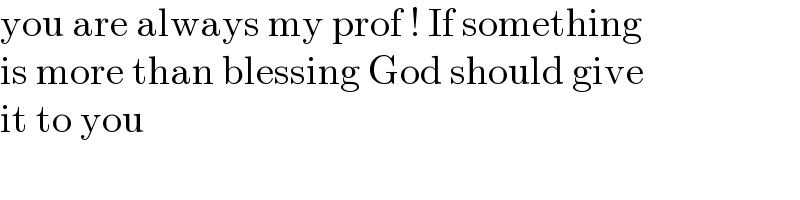
$$\mathrm{you}\:\mathrm{are}\:\mathrm{always}\:\mathrm{my}\:\mathrm{prof}\:!\:\mathrm{If}\:\mathrm{something} \\ $$$$\mathrm{is}\:\mathrm{more}\:\mathrm{than}\:\mathrm{blessing}\:\mathrm{God}\:\mathrm{should}\:\mathrm{give} \\ $$$$\mathrm{it}\:\mathrm{to}\:\mathrm{you} \\ $$
Commented by mr W last updated on 14/Feb/21

$${God}\:{bless}\:{you}\:{too}! \\ $$
