Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 132240 by bemath last updated on 12/Feb/21

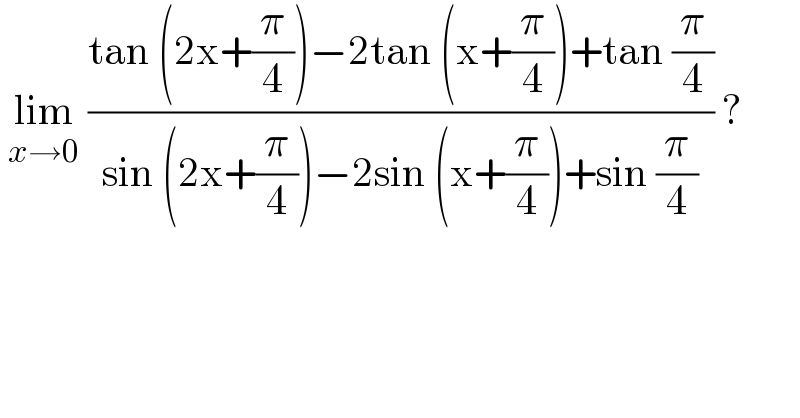
lim_(x→0) ((tan (2x+(π/4))−2tan (x+(π/4))+tan (π/4))/(sin (2x+(π/4))−2sin (x+(π/4))+sin (π/4))) ?

$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}\:\left(\mathrm{2x}+\frac{\pi}{\mathrm{4}}\right)−\mathrm{2tan}\:\left(\mathrm{x}+\frac{\pi}{\mathrm{4}}\right)+\mathrm{tan}\:\frac{\pi}{\mathrm{4}}}{\mathrm{sin}\:\left(\mathrm{2x}+\frac{\pi}{\mathrm{4}}\right)−\mathrm{2sin}\:\left(\mathrm{x}+\frac{\pi}{\mathrm{4}}\right)+\mathrm{sin}\:\frac{\pi}{\mathrm{4}}}\:? \\ $$$$ \\ $$

Answered by EDWIN88 last updated on 13/Feb/21

lim_(x→0) ((2sec^2 (2x+(π/4))−2sec^2 (x+(π/4)))/(2cos (2x+(π/4))−2cos (x+(π/4)))) = lim_(x→0) ((cos^2 (x+(π/4))−cos^2 (2x+(π/4)))/([ cos (2x+(π/4)).cos (x+(π/4))]^2 [cos (2x+(π/4))−cos (x+(π/4))])) = lim_(x→0) ((−[ cos (x+(π/4))+cos (2x+(π/4)) ])/([ cos (2x+(π/4)).cos (x+(π/4))]^2 )) = −((√2)/(((1/2))^2 )) = −4(√2)

$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2sec}\:^{\mathrm{2}} \left(\mathrm{2x}+\frac{\pi}{\mathrm{4}}\right)−\mathrm{2sec}\:^{\mathrm{2}} \left(\mathrm{x}+\frac{\pi}{\mathrm{4}}\right)}{\mathrm{2cos}\:\left(\mathrm{2x}+\frac{\pi}{\mathrm{4}}\right)−\mathrm{2cos}\:\left(\mathrm{x}+\frac{\pi}{\mathrm{4}}\right)} \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{cos}\:^{\mathrm{2}} \left(\mathrm{x}+\frac{\pi}{\mathrm{4}}\right)−\mathrm{cos}\:^{\mathrm{2}} \left(\mathrm{2x}+\frac{\pi}{\mathrm{4}}\right)}{\left[\:\mathrm{cos}\:\left(\mathrm{2x}+\frac{\pi}{\mathrm{4}}\right).\mathrm{cos}\:\left(\mathrm{x}+\frac{\pi}{\mathrm{4}}\right)\right]^{\mathrm{2}} \left[\mathrm{cos}\:\left(\mathrm{2x}+\frac{\pi}{\mathrm{4}}\right)−\mathrm{cos}\:\left(\mathrm{x}+\frac{\pi}{\mathrm{4}}\right)\right]} \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\left[\:\mathrm{cos}\:\left(\mathrm{x}+\frac{\pi}{\mathrm{4}}\right)+\mathrm{cos}\:\left(\mathrm{2x}+\frac{\pi}{\mathrm{4}}\right)\:\right]}{\left[\:\mathrm{cos}\:\left(\mathrm{2x}+\frac{\pi}{\mathrm{4}}\right).\mathrm{cos}\:\left(\mathrm{x}+\frac{\pi}{\mathrm{4}}\right)\right]^{\mathrm{2}} } \\ $$$$=\:−\frac{\sqrt{\mathrm{2}}}{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }\:=\:−\mathrm{4}\sqrt{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com