
Question Number 131684 by aurpeyz last updated on 07/Feb/21

Answered by ajfour last updated on 07/Feb/21

$$\:\:\:\:\:\:\:\:\:\:\:\:\:\circleddash\left(−\mathrm{2}\mu{C}\:\right)\:\:\:\:\:\:\:\:\:\:\:\oplus\left(\mathrm{10}\mu{C}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{4}\pi\epsilon_{\mathrm{0}} }\frac{\mid{q}_{\mathrm{3}} {q}_{\mathrm{2}} \mid}{{r}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{4}\pi\epsilon_{\mathrm{0}} }\frac{\mid{q}_{\mathrm{3}} {q}_{\mathrm{1}} \mid}{\left({r}+\mathrm{1}{m}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:\frac{{r}+\mathrm{1}{m}}{{r}}=\sqrt{\mid\frac{{q}_{\mathrm{1}} }{{q}_{\mathrm{2}} }\mid} \\ $$$$\:\:\mathrm{1}+\frac{\mathrm{1}{m}}{{r}}=\sqrt{\mathrm{5}} \\ $$$${r}=\frac{\mathrm{1}{m}}{\:\sqrt{\mathrm{5}}−\mathrm{1}}=\frac{\mathrm{1}{m}\left(\sqrt{\mathrm{5}}+\mathrm{1}\right)}{\mathrm{4}} \\ $$$${r}=\frac{\mathrm{1}{m}\left(\mathrm{3}.\mathrm{236}\right)}{\mathrm{4}}=\mathrm{0}.\mathrm{809}{m} \\ $$$${x}=−\mathrm{0}.\mathrm{809}{m}\:\:\:\:\:\:\left({A}\right) \\ $$
Commented by aurpeyz last updated on 08/Feb/21

$${thank}\:{you} \\ $$
Answered by Dwaipayan Shikari last updated on 07/Feb/21
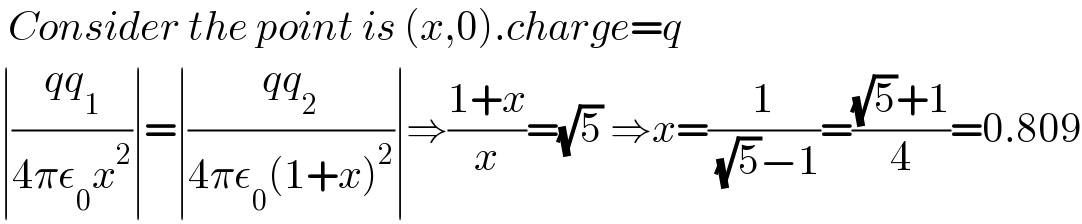
$$\:{Consider}\:{the}\:{point}\:{is}\:\left({x},\mathrm{0}\right).{charge}={q} \\ $$$$\mid\frac{{qq}_{\mathrm{1}} }{\mathrm{4}\pi\epsilon_{\mathrm{0}} {x}^{\mathrm{2}} }\mid=\mid\frac{{qq}_{\mathrm{2}} }{\mathrm{4}\pi\epsilon_{\mathrm{0}} \left(\mathrm{1}+{x}\right)^{\mathrm{2}} }\mid\Rightarrow\frac{\mathrm{1}+{x}}{{x}}=\sqrt{\mathrm{5}}\:\Rightarrow{x}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}−\mathrm{1}}=\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{4}}=\mathrm{0}.\mathrm{809} \\ $$
