
Question Number 131595 by Algoritm last updated on 06/Feb/21
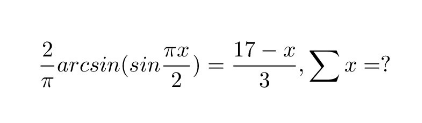
Commented by Algoritm last updated on 06/Feb/21
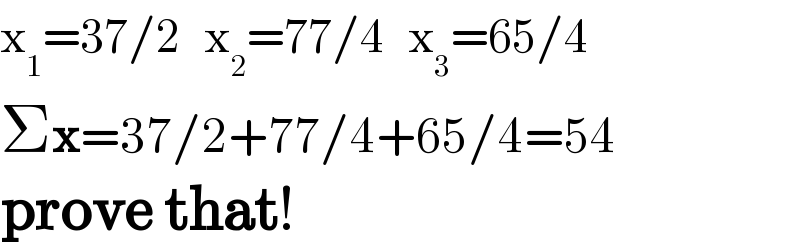
$$\mathrm{x}_{\mathrm{1}} =\mathrm{37}/\mathrm{2}\:\:\:\mathrm{x}_{\mathrm{2}} =\mathrm{77}/\mathrm{4}\:\:\:\mathrm{x}_{\mathrm{3}} =\mathrm{65}/\mathrm{4} \\ $$$$\Sigma\boldsymbol{\mathrm{x}}=\mathrm{37}/\mathrm{2}+\mathrm{77}/\mathrm{4}+\mathrm{65}/\mathrm{4}=\mathrm{54}\:\: \\ $$$$\boldsymbol{\mathrm{prove}}\:\boldsymbol{\mathrm{that}}! \\ $$
Answered by mr W last updated on 06/Feb/21
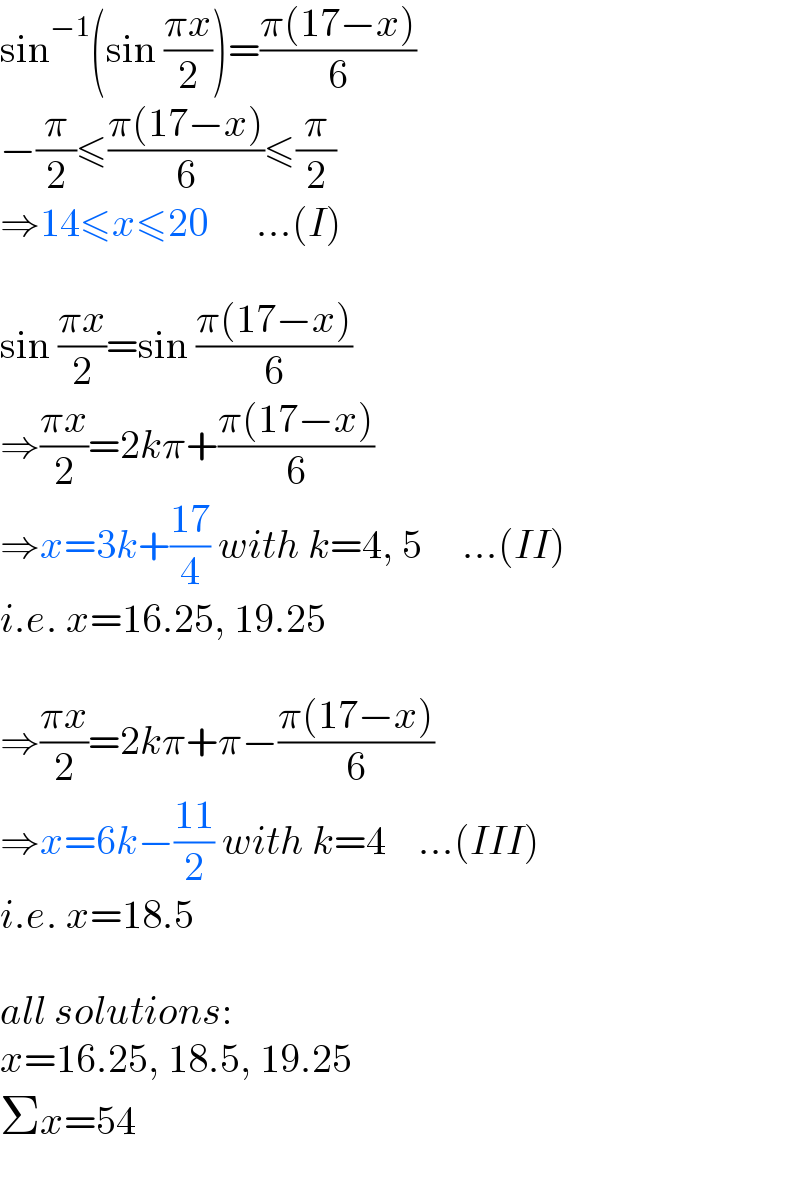
$$\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{sin}\:\frac{\pi{x}}{\mathrm{2}}\right)=\frac{\pi\left(\mathrm{17}−{x}\right)}{\mathrm{6}} \\ $$$$−\frac{\pi}{\mathrm{2}}\leqslant\frac{\pi\left(\mathrm{17}−{x}\right)}{\mathrm{6}}\leqslant\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{14}\leqslant{x}\leqslant\mathrm{20}\:\:\:\:\:\:...\left({I}\right) \\ $$$$ \\ $$$$\mathrm{sin}\:\frac{\pi{x}}{\mathrm{2}}=\mathrm{sin}\:\frac{\pi\left(\mathrm{17}−{x}\right)}{\mathrm{6}} \\ $$$$\Rightarrow\frac{\pi{x}}{\mathrm{2}}=\mathrm{2}{k}\pi+\frac{\pi\left(\mathrm{17}−{x}\right)}{\mathrm{6}} \\ $$$$\Rightarrow{x}=\mathrm{3}{k}+\frac{\mathrm{17}}{\mathrm{4}}\:{with}\:{k}=\mathrm{4},\:\mathrm{5}\:\:\:\:\:...\left({II}\right) \\ $$$${i}.{e}.\:{x}=\mathrm{16}.\mathrm{25},\:\mathrm{19}.\mathrm{25} \\ $$$$ \\ $$$$\Rightarrow\frac{\pi{x}}{\mathrm{2}}=\mathrm{2}{k}\pi+\pi−\frac{\pi\left(\mathrm{17}−{x}\right)}{\mathrm{6}} \\ $$$$\Rightarrow{x}=\mathrm{6}{k}−\frac{\mathrm{11}}{\mathrm{2}}\:{with}\:{k}=\mathrm{4}\:\:\:\:...\left({III}\right) \\ $$$${i}.{e}.\:{x}=\mathrm{18}.\mathrm{5} \\ $$$$ \\ $$$${all}\:{solutions}: \\ $$$${x}=\mathrm{16}.\mathrm{25},\:\mathrm{18}.\mathrm{5},\:\mathrm{19}.\mathrm{25} \\ $$$$\Sigma{x}=\mathrm{54} \\ $$
