
Question Number 131581 by mnjuly1970 last updated on 06/Feb/21
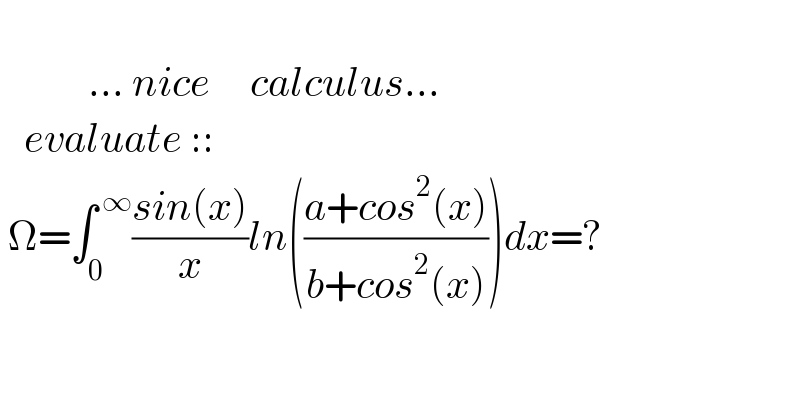
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:...\:{nice}\:\:\:\:\:{calculus}... \\ $$$$\:\:\:{evaluate}\::: \\ $$$$\:\Omega=\int_{\mathrm{0}} ^{\:\infty} \frac{{sin}\left({x}\right)}{{x}}{ln}\left(\frac{{a}+{cos}^{\mathrm{2}} \left({x}\right)}{{b}+{cos}^{\mathrm{2}} \left({x}\right)}\right){dx}=? \\ $$$$ \\ $$
Commented by Dwaipayan Shikari last updated on 06/Feb/21
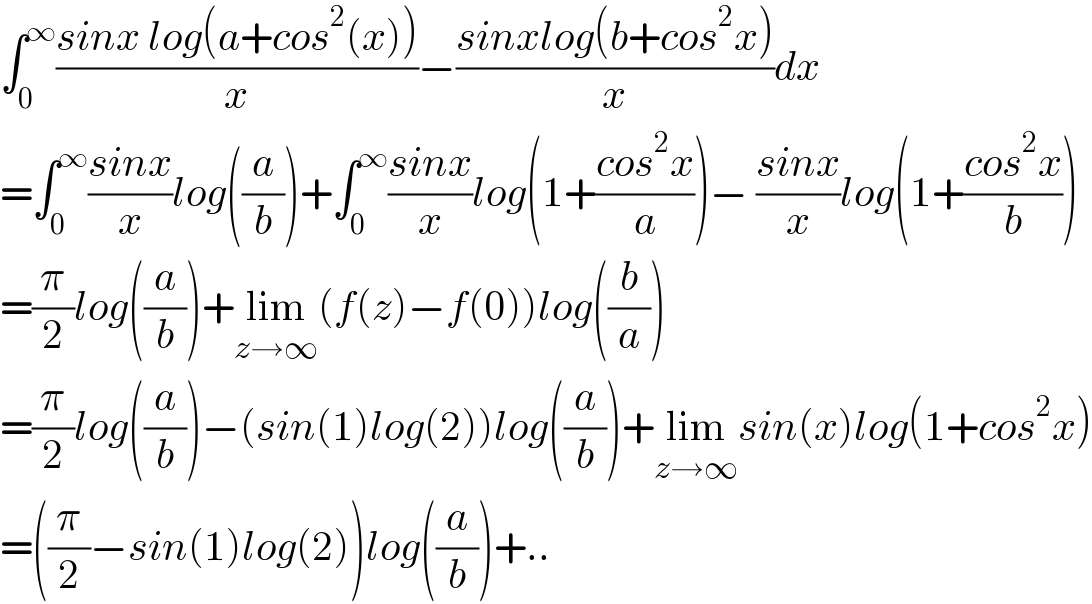
$$\int_{\mathrm{0}} ^{\infty} \frac{{sinx}\:{log}\left({a}+{cos}^{\mathrm{2}} \left({x}\right)\right)}{{x}}−\frac{{sinxlog}\left({b}+{cos}^{\mathrm{2}} {x}\right)}{{x}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{{sinx}}{{x}}{log}\left(\frac{{a}}{{b}}\right)+\int_{\mathrm{0}} ^{\infty} \frac{{sinx}}{{x}}{log}\left(\mathrm{1}+\frac{{cos}^{\mathrm{2}} {x}}{{a}}\right)−\:\frac{{sinx}}{{x}}{log}\left(\mathrm{1}+\frac{{cos}^{\mathrm{2}} {x}}{{b}}\right) \\ $$$$=\frac{\pi}{\mathrm{2}}{log}\left(\frac{{a}}{{b}}\right)+\underset{{z}\rightarrow\infty} {\mathrm{lim}}\left({f}\left({z}\right)−{f}\left(\mathrm{0}\right)\right){log}\left(\frac{{b}}{{a}}\right) \\ $$$$=\frac{\pi}{\mathrm{2}}{log}\left(\frac{{a}}{{b}}\right)−\left({sin}\left(\mathrm{1}\right){log}\left(\mathrm{2}\right)\right){log}\left(\frac{{a}}{{b}}\right)+\underset{{z}\rightarrow\infty} {\mathrm{lim}}{sin}\left({x}\right){log}\left(\mathrm{1}+{cos}^{\mathrm{2}} {x}\right) \\ $$$$=\left(\frac{\pi}{\mathrm{2}}−{sin}\left(\mathrm{1}\right){log}\left(\mathrm{2}\right)\right){log}\left(\frac{{a}}{{b}}\right)+.. \\ $$
