
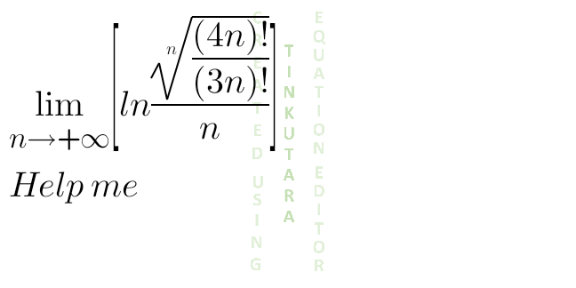
Question Number 131374 by shaker last updated on 04/Feb/21
Answered by MJS_new last updated on 04/Feb/21
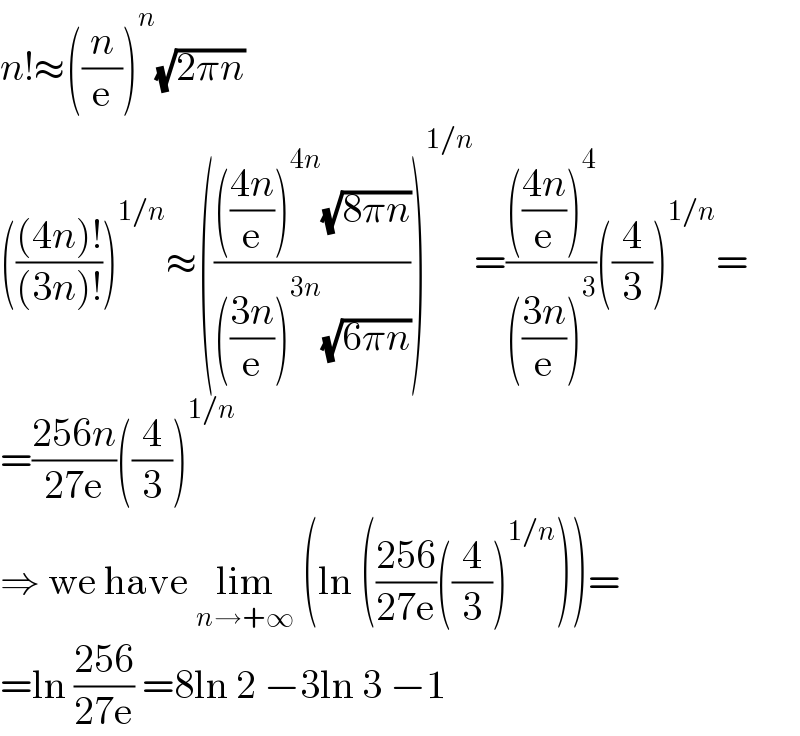
$${n}!\approx\left(\frac{{n}}{\mathrm{e}}\right)^{{n}} \sqrt{\mathrm{2}\pi{n}} \\ $$$$\left(\frac{\left(\mathrm{4}{n}\right)!}{\left(\mathrm{3}{n}\right)!}\right)^{\mathrm{1}/{n}} \approx\left(\frac{\left(\frac{\mathrm{4}{n}}{\mathrm{e}}\right)^{\mathrm{4}{n}} \sqrt{\mathrm{8}\pi{n}}}{\left(\frac{\mathrm{3}{n}}{\mathrm{e}}\right)^{\mathrm{3}{n}} \sqrt{\mathrm{6}\pi{n}}}\right)^{\mathrm{1}/{n}} =\frac{\left(\frac{\mathrm{4}{n}}{\mathrm{e}}\right)^{\mathrm{4}} }{\left(\frac{\mathrm{3}{n}}{\mathrm{e}}\right)^{\mathrm{3}} }\left(\frac{\mathrm{4}}{\mathrm{3}}\right)^{\mathrm{1}/{n}} = \\ $$$$=\frac{\mathrm{256}{n}}{\mathrm{27e}}\left(\frac{\mathrm{4}}{\mathrm{3}}\right)^{\mathrm{1}/{n}} \\ $$$$\Rightarrow\:\mathrm{we}\:\mathrm{have}\:\underset{{n}\rightarrow+\infty} {\mathrm{lim}}\:\left(\mathrm{ln}\:\left(\frac{\mathrm{256}}{\mathrm{27e}}\left(\frac{\mathrm{4}}{\mathrm{3}}\right)^{\mathrm{1}/{n}} \right)\right)= \\ $$$$=\mathrm{ln}\:\frac{\mathrm{256}}{\mathrm{27e}}\:=\mathrm{8ln}\:\mathrm{2}\:−\mathrm{3ln}\:\mathrm{3}\:−\mathrm{1} \\ $$
Answered by aleks041103 last updated on 04/Feb/21
![Stirling′s approximation (n)!∼ n^n e^(−n) =((n/e))^n Proof: ln(x!)=Σ_(y=1) ^x ln(y)=Σ_(y=1) ^x ln(y)Δy≈∫_1 ^x ln(y)dy Δy=1 ∫_1 ^x ln(y)dy=yln(y)∣_1 ^x −∫_1 ^x yd(ln(y))= =xln(x)−∫_1 ^x dy=xln(x)−x+1 x≫1, ln(x!)∼ln(x^x e^(−x) ) Q.E.D lim_(n→∞) [ln((((((4n)!)/((3n)!)))^(1/n) /n))]= =lim_(n→∞) [ln(((((((4^4 n^4 e^3 )/(3^3 n^3 e^4 )))^n ))^(1/n) /n))]= =lim_(n→∞) [ln(((256n)/(27ne)))]=ln(256/27)+ln(1/e)= =ln(((256)/(27)))−1](Q131380.png)
$${Stirling}'{s}\:{approximation} \\ $$$$\left({n}\right)!\sim\:{n}^{{n}} {e}^{−{n}} =\left(\frac{{n}}{{e}}\right)^{{n}} \\ $$$${Proof}: \\ $$$${ln}\left({x}!\right)=\underset{{y}=\mathrm{1}} {\overset{{x}} {\sum}}{ln}\left({y}\right)=\underset{{y}=\mathrm{1}} {\overset{{x}} {\sum}}{ln}\left({y}\right)\Delta{y}\approx\underset{\mathrm{1}} {\overset{{x}} {\int}}{ln}\left({y}\right){dy} \\ $$$$\Delta{y}=\mathrm{1} \\ $$$$\underset{\mathrm{1}} {\overset{{x}} {\int}}{ln}\left({y}\right){dy}={yln}\left({y}\right)\mid_{\mathrm{1}} ^{{x}} −\underset{\mathrm{1}} {\overset{{x}} {\int}}{yd}\left({ln}\left({y}\right)\right)= \\ $$$$={xln}\left({x}\right)−\underset{\mathrm{1}} {\overset{{x}} {\int}}{dy}={xln}\left({x}\right)−{x}+\mathrm{1} \\ $$$${x}\gg\mathrm{1},\:{ln}\left({x}!\right)\sim{ln}\left({x}^{{x}} {e}^{−{x}} \right) \\ $$$${Q}.{E}.{D} \\ $$$$ \\ $$$$\underset{{n}\rightarrow\infty} {{lim}}\left[{ln}\left(\frac{\sqrt[{{n}}]{\frac{\left(\mathrm{4}{n}\right)!}{\left(\mathrm{3}{n}\right)!}}}{{n}}\right)\right]= \\ $$$$=\underset{{n}\rightarrow\infty} {{lim}}\left[{ln}\left(\frac{\sqrt[{{n}}]{\left(\frac{\mathrm{4}^{\mathrm{4}} {n}^{\mathrm{4}} {e}^{\mathrm{3}} }{\mathrm{3}^{\mathrm{3}} {n}^{\mathrm{3}} {e}^{\mathrm{4}} }\right)^{{n}} }}{{n}}\right)\right]= \\ $$$$=\underset{{n}\rightarrow\infty} {{lim}}\left[{ln}\left(\frac{\mathrm{256}{n}}{\mathrm{27}{ne}}\right)\right]={ln}\left(\mathrm{256}/\mathrm{27}\right)+{ln}\left(\mathrm{1}/{e}\right)= \\ $$$$={ln}\left(\frac{\mathrm{256}}{\mathrm{27}}\right)−\mathrm{1} \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 04/Feb/21
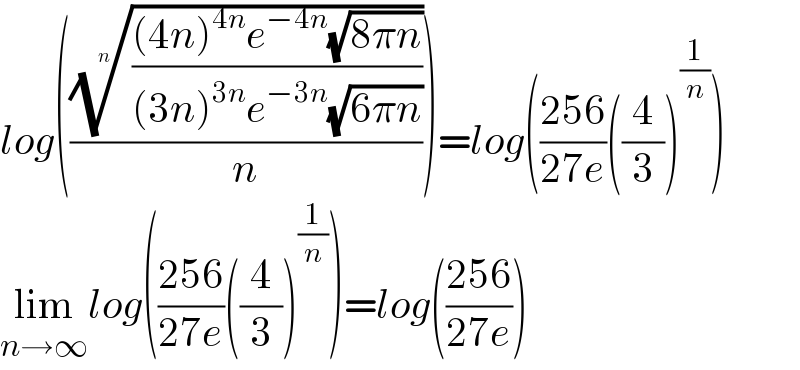
$${log}\left(\frac{\sqrt[{{n}}]{\frac{\left(\mathrm{4}{n}\right)^{\mathrm{4}{n}} {e}^{−\mathrm{4}{n}} \sqrt{\mathrm{8}\pi{n}}}{\left(\mathrm{3}{n}\right)^{\mathrm{3}{n}} {e}^{−\mathrm{3}{n}} \sqrt{\mathrm{6}\pi{n}}}}}{{n}}\right)={log}\left(\frac{\mathrm{256}}{\mathrm{27}{e}}\left(\frac{\mathrm{4}}{\mathrm{3}}\right)^{\frac{\mathrm{1}}{{n}}} \right) \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}{log}\left(\frac{\mathrm{256}}{\mathrm{27}{e}}\left(\frac{\mathrm{4}}{\mathrm{3}}\right)^{\frac{\mathrm{1}}{{n}}} \right)={log}\left(\frac{\mathrm{256}}{\mathrm{27}{e}}\right) \\ $$
