
Question Number 131218 by shaker last updated on 02/Feb/21
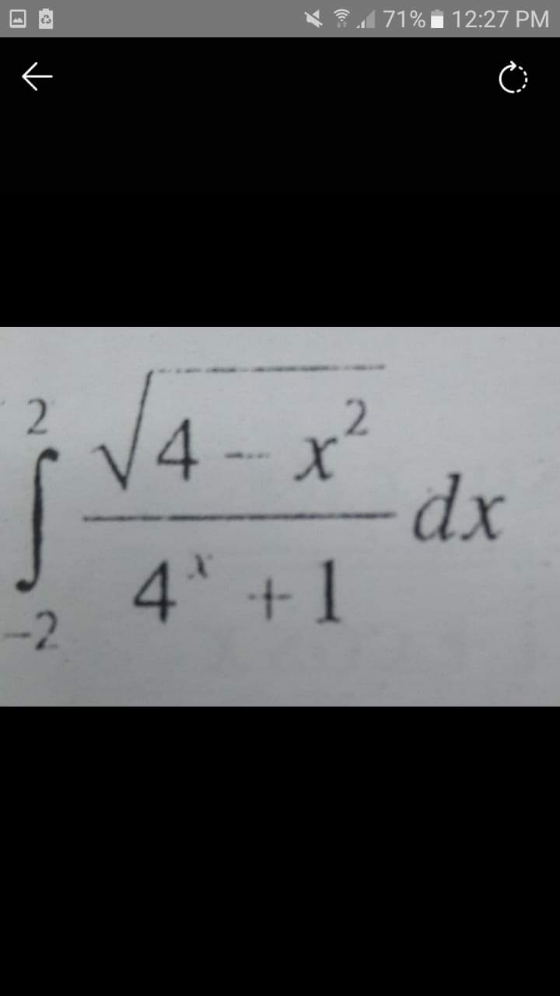
Answered by mathmax by abdo last updated on 02/Feb/21
![I =∫_(−2) ^2 ((√(4−x^2 ))/(4^x +1)) ⇒I =_(x=−t) ∫_(−2) ^2 ((√(4−t^2 ))/(4^(−t) +1))dt ⇒ 2I =∫_(−2) ^2 ((√(4−x^2 ))/(4^x +1))+∫_(−2) ^2 ((√(4−x^2 ))/(4^(−x) +1))dx =∫_(−2) ^2 (√(4−x^2 ))(((4^(−x) +1+4^x +1)/(1+4^x +4^(−x) +1)))dx =∫_(−2) ^2 (√(4−x^2 ))dx =2∫_0 ^2 (√(4−x^2 ))dx =_(x=2sinθ) 2∫_0 ^(π/2) 2cosθ(2cosθ)dθ =8∫_0 ^(π/2) cos^2 θ dθ =4∫_0 ^(π/2) (1+cos(2θ))dθ =2π +2[sin(2θ)]_0 ^(π/2) =2π ⇒ I =π](Q131237.png)
$$\mathrm{I}\:=\int_{−\mathrm{2}} ^{\mathrm{2}} \:\frac{\sqrt{\mathrm{4}−\mathrm{x}^{\mathrm{2}} }}{\mathrm{4}^{\mathrm{x}} \:+\mathrm{1}}\:\Rightarrow\mathrm{I}\:=_{\mathrm{x}=−\mathrm{t}} \:\:\:\int_{−\mathrm{2}} ^{\mathrm{2}} \:\frac{\sqrt{\mathrm{4}−\mathrm{t}^{\mathrm{2}} }}{\mathrm{4}^{−\mathrm{t}} \:+\mathrm{1}}\mathrm{dt}\:\:\Rightarrow \\ $$$$\mathrm{2I}\:=\int_{−\mathrm{2}} ^{\mathrm{2}} \:\frac{\sqrt{\mathrm{4}−\mathrm{x}^{\mathrm{2}} }}{\mathrm{4}^{\mathrm{x}} \:+\mathrm{1}}+\int_{−\mathrm{2}} ^{\mathrm{2}} \:\frac{\sqrt{\mathrm{4}−\mathrm{x}^{\mathrm{2}} }}{\mathrm{4}^{−\mathrm{x}} \:+\mathrm{1}}\mathrm{dx}\:=\int_{−\mathrm{2}} ^{\mathrm{2}} \sqrt{\mathrm{4}−\mathrm{x}^{\mathrm{2}} }\left(\frac{\mathrm{4}^{−\mathrm{x}} \:+\mathrm{1}+\mathrm{4}^{\mathrm{x}} \:+\mathrm{1}}{\mathrm{1}+\mathrm{4}^{\mathrm{x}} \:+\mathrm{4}^{−\mathrm{x}} \:+\mathrm{1}}\right)\mathrm{dx} \\ $$$$=\int_{−\mathrm{2}} ^{\mathrm{2}} \:\sqrt{\mathrm{4}−\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{2}} \sqrt{\mathrm{4}−\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:=_{\mathrm{x}=\mathrm{2sin}\theta} \:\:\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{2cos}\theta\left(\mathrm{2cos}\theta\right)\mathrm{d}\theta \\ $$$$=\mathrm{8}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}^{\mathrm{2}} \theta\:\mathrm{d}\theta\:=\mathrm{4}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}+\mathrm{cos}\left(\mathrm{2}\theta\right)\right)\mathrm{d}\theta\:=\mathrm{2}\pi\:+\mathrm{2}\left[\mathrm{sin}\left(\mathrm{2}\theta\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:=\mathrm{2}\pi\:\Rightarrow \\ $$$$\mathrm{I}\:=\pi \\ $$
Answered by Ar Brandon last updated on 02/Feb/21
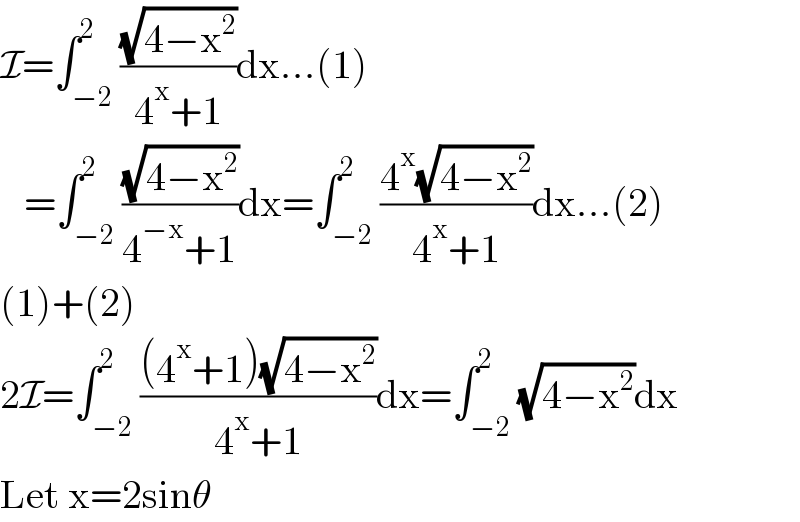
$$\mathcal{I}=\int_{−\mathrm{2}} ^{\mathrm{2}} \frac{\sqrt{\mathrm{4}−\mathrm{x}^{\mathrm{2}} }}{\mathrm{4}^{\mathrm{x}} +\mathrm{1}}\mathrm{dx}...\left(\mathrm{1}\right) \\ $$$$\:\:\:=\int_{−\mathrm{2}} ^{\mathrm{2}} \frac{\sqrt{\mathrm{4}−\mathrm{x}^{\mathrm{2}} }}{\mathrm{4}^{−\mathrm{x}} +\mathrm{1}}\mathrm{dx}=\int_{−\mathrm{2}} ^{\mathrm{2}} \frac{\mathrm{4}^{\mathrm{x}} \sqrt{\mathrm{4}−\mathrm{x}^{\mathrm{2}} }}{\mathrm{4}^{\mathrm{x}} +\mathrm{1}}\mathrm{dx}...\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)+\left(\mathrm{2}\right) \\ $$$$\mathrm{2}\mathcal{I}=\int_{−\mathrm{2}} ^{\mathrm{2}} \frac{\left(\mathrm{4}^{\mathrm{x}} +\mathrm{1}\right)\sqrt{\mathrm{4}−\mathrm{x}^{\mathrm{2}} }}{\mathrm{4}^{\mathrm{x}} +\mathrm{1}}\mathrm{dx}=\int_{−\mathrm{2}} ^{\mathrm{2}} \sqrt{\mathrm{4}−\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$\mathrm{Let}\:\mathrm{x}=\mathrm{2sin}\theta \\ $$
Commented by Ar Brandon last updated on 02/Feb/21
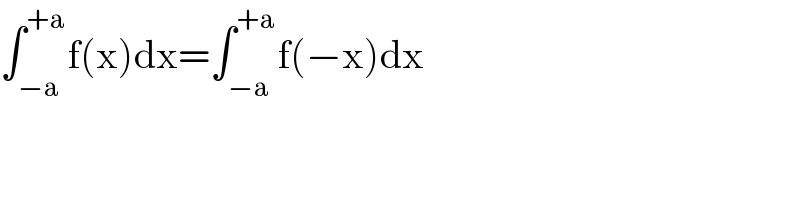
$$\int_{−\mathrm{a}} ^{+\mathrm{a}} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\int_{−\mathrm{a}} ^{+\mathrm{a}} \mathrm{f}\left(−\mathrm{x}\right)\mathrm{dx} \\ $$
