
Question Number 13121 by tawa tawa last updated on 14/May/17
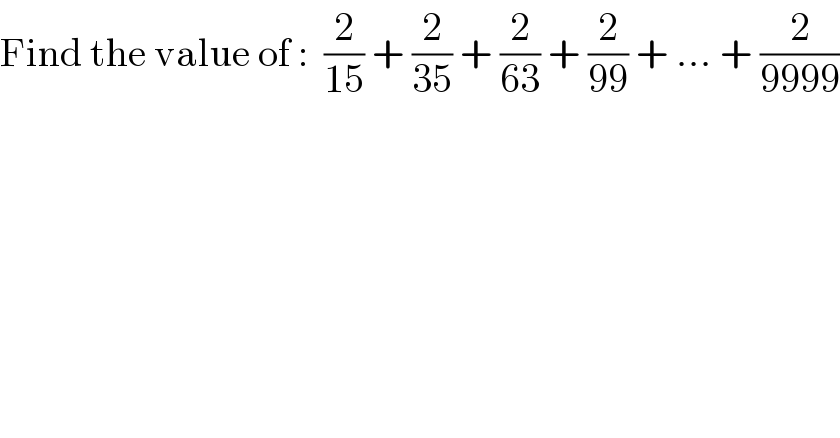
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\::\:\:\frac{\mathrm{2}}{\mathrm{15}}\:+\:\frac{\mathrm{2}}{\mathrm{35}}\:+\:\frac{\mathrm{2}}{\mathrm{63}}\:+\:\frac{\mathrm{2}}{\mathrm{99}}\:+\:...\:+\:\frac{\mathrm{2}}{\mathrm{9999}} \\ $$
Answered by nume1114 last updated on 15/May/17
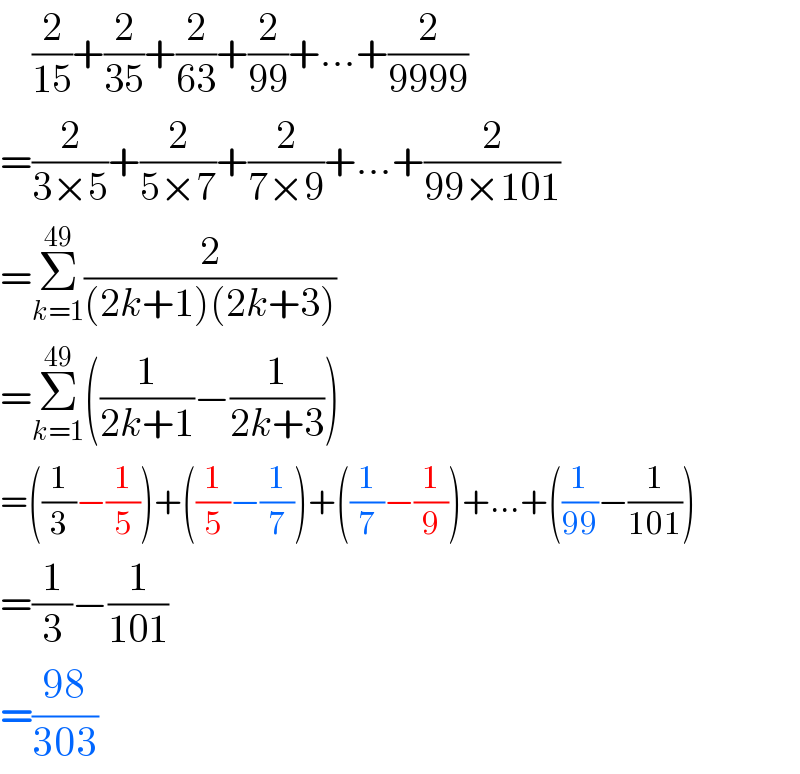
$$\:\:\:\:\frac{\mathrm{2}}{\mathrm{15}}+\frac{\mathrm{2}}{\mathrm{35}}+\frac{\mathrm{2}}{\mathrm{63}}+\frac{\mathrm{2}}{\mathrm{99}}+...+\frac{\mathrm{2}}{\mathrm{9999}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}×\mathrm{5}}+\frac{\mathrm{2}}{\mathrm{5}×\mathrm{7}}+\frac{\mathrm{2}}{\mathrm{7}×\mathrm{9}}+...+\frac{\mathrm{2}}{\mathrm{99}×\mathrm{101}} \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{\mathrm{49}} {\sum}}\frac{\mathrm{2}}{\left(\mathrm{2}{k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{3}\right)} \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{\mathrm{49}} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{3}}\right) \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{5}}\right)+\left(\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{7}}\right)+\left(\frac{\mathrm{1}}{\mathrm{7}}−\frac{\mathrm{1}}{\mathrm{9}}\right)+...+\left(\frac{\mathrm{1}}{\mathrm{99}}−\frac{\mathrm{1}}{\mathrm{101}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{101}} \\ $$$$=\frac{\mathrm{98}}{\mathrm{303}} \\ $$
Commented by tawa tawa last updated on 15/May/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by nume1114 last updated on 15/May/17
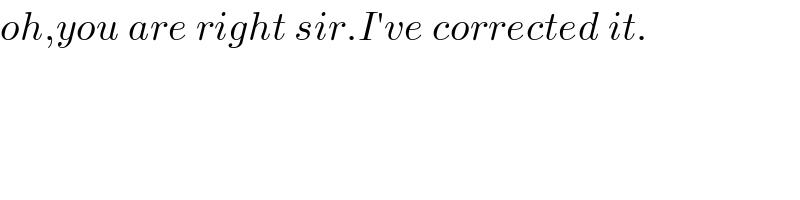
$${oh},{you}\:{are}\:{right}\:{sir}.{I}'{ve}\:{corrected}\:{it}. \\ $$
Commented by RasheedSindhi last updated on 15/May/17

$$\mathcal{N}{i}\mathcal{CE}! \\ $$
Commented by tawa tawa last updated on 15/May/17
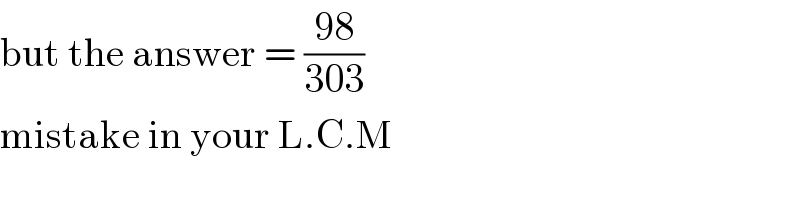
$$\mathrm{but}\:\mathrm{the}\:\mathrm{answer}\:=\:\frac{\mathrm{98}}{\mathrm{303}} \\ $$$$\mathrm{mistake}\:\mathrm{in}\:\mathrm{your}\:\mathrm{L}.\mathrm{C}.\mathrm{M} \\ $$
