
Question Number 131146 by EDWIN88 last updated on 02/Feb/21
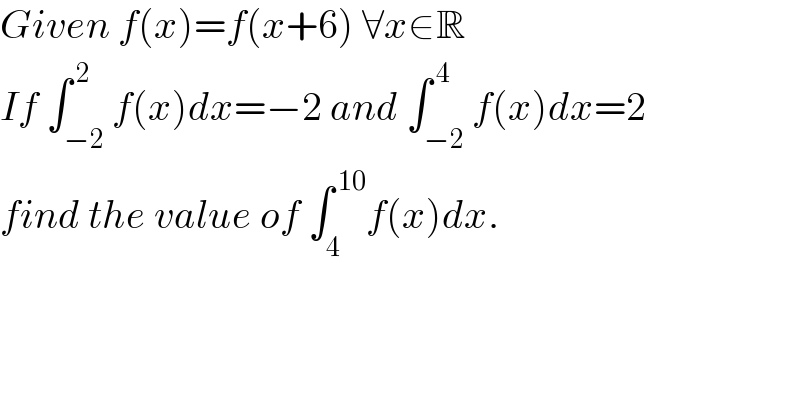
$${Given}\:{f}\left({x}\right)={f}\left({x}+\mathrm{6}\right)\:\forall{x}\in\mathbb{R} \\ $$$${If}\:\int_{−\mathrm{2}} ^{\:\mathrm{2}} {f}\left({x}\right){dx}=−\mathrm{2}\:{and}\:\int_{−\mathrm{2}} ^{\:\mathrm{4}} {f}\left({x}\right){dx}=\mathrm{2} \\ $$$${find}\:{the}\:{value}\:{of}\:\int_{\mathrm{4}} ^{\:\mathrm{10}} {f}\left({x}\right){dx}. \\ $$
Commented by EDWIN88 last updated on 02/Feb/21
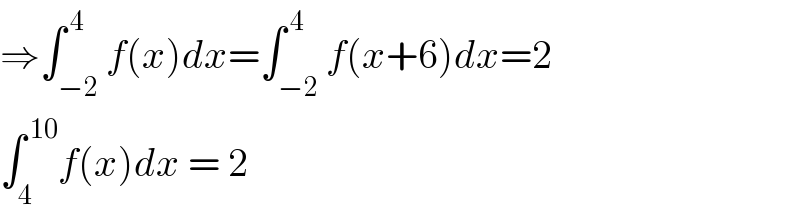
$$\Rightarrow\int_{−\mathrm{2}} ^{\:\mathrm{4}} {f}\left({x}\right){dx}=\int_{−\mathrm{2}} ^{\:\mathrm{4}} {f}\left({x}+\mathrm{6}\right){dx}=\mathrm{2} \\ $$$$\int_{\mathrm{4}} ^{\:\mathrm{10}} {f}\left({x}\right){dx}\:=\:\mathrm{2} \\ $$
Answered by Ar Brandon last updated on 02/Feb/21
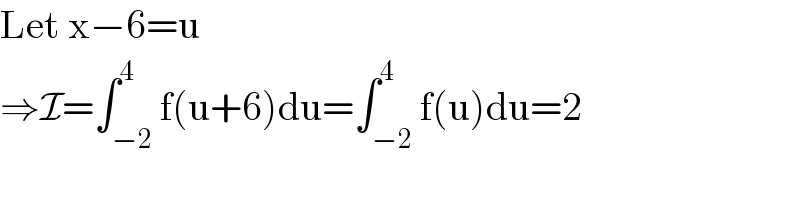
$$\mathrm{Let}\:\mathrm{x}−\mathrm{6}=\mathrm{u} \\ $$$$\Rightarrow\mathcal{I}=\int_{−\mathrm{2}} ^{\mathrm{4}} \mathrm{f}\left(\mathrm{u}+\mathrm{6}\right)\mathrm{du}=\int_{−\mathrm{2}} ^{\mathrm{4}} \mathrm{f}\left(\mathrm{u}\right)\mathrm{du}=\mathrm{2} \\ $$
