
Question Number 131084 by greg_ed last updated on 01/Feb/21
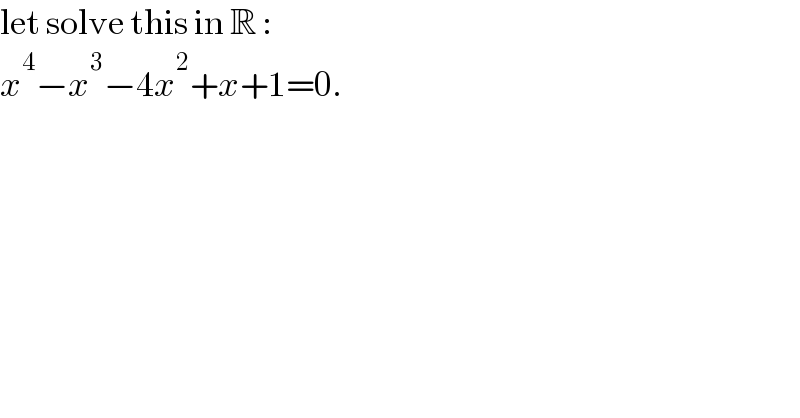
$$\mathrm{let}\:\mathrm{solve}\:\mathrm{this}\:\mathrm{in}\:\mathbb{R}\::\: \\ $$$${x}^{\mathrm{4}} −{x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} +{x}+\mathrm{1}=\mathrm{0}. \\ $$
Answered by liberty last updated on 01/Feb/21

$$\mathrm{x}_{\mathrm{1}} =\mathrm{2}.\mathrm{414} \\ $$$$\mathrm{x}_{\mathrm{2}} =\mathrm{0}.\mathrm{618} \\ $$$$\mathrm{x}_{\mathrm{3}} =−\mathrm{0}.\mathrm{414} \\ $$$$\mathrm{x}_{\mathrm{4}} =−\mathrm{1}.\mathrm{618} \\ $$
Answered by MJS_new last updated on 01/Feb/21
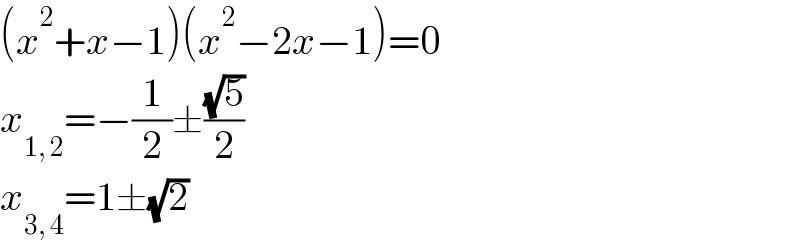
$$\left({x}^{\mathrm{2}} +{x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{1}\right)=\mathrm{0} \\ $$$${x}_{\mathrm{1},\:\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${x}_{\mathrm{3},\:\mathrm{4}} =\mathrm{1}\pm\sqrt{\mathrm{2}} \\ $$
