
Question Number 131064 by shaker last updated on 01/Feb/21
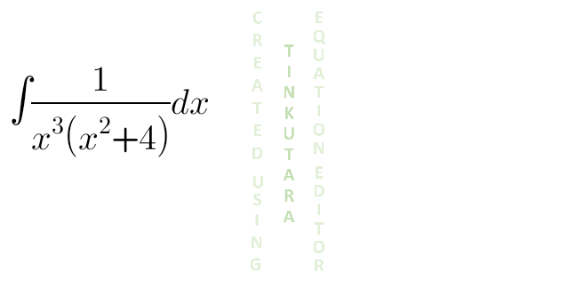
Answered by Dwaipayan Shikari last updated on 01/Feb/21
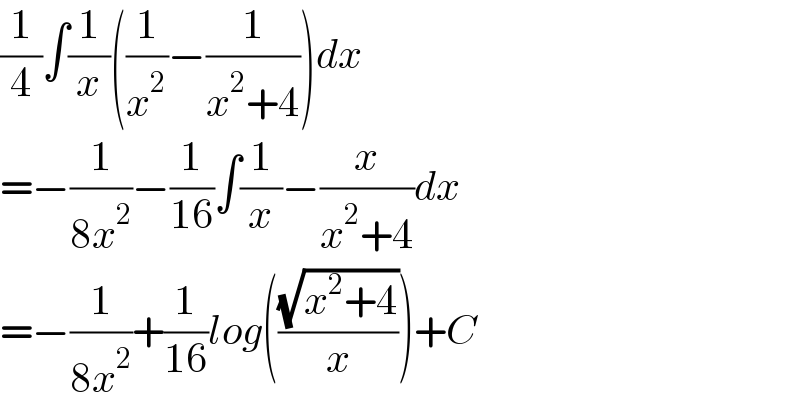
$$\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{1}}{{x}}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{4}}\right){dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{8}{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{16}}\int\frac{\mathrm{1}}{{x}}−\frac{{x}}{{x}^{\mathrm{2}} +\mathrm{4}}{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{8}{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{16}}{log}\left(\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{4}}}{{x}}\right)+{C} \\ $$
Answered by benjo_mathlover last updated on 01/Feb/21
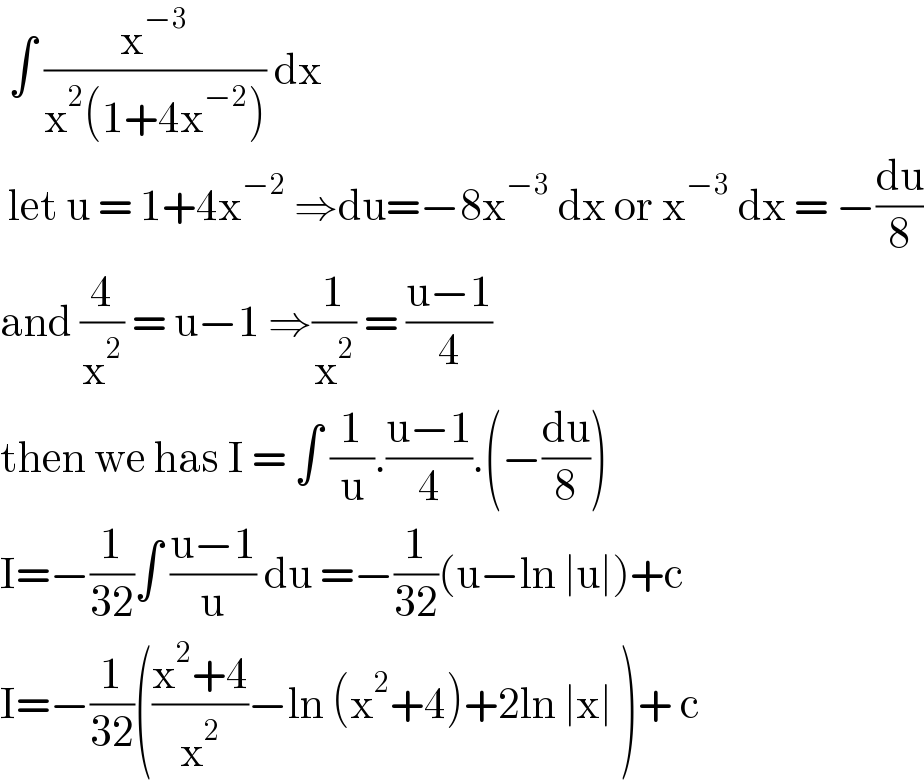
$$\:\int\:\frac{\mathrm{x}^{−\mathrm{3}} }{\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{4x}^{−\mathrm{2}} \right)}\:\mathrm{dx}\: \\ $$$$\:\mathrm{let}\:\mathrm{u}\:=\:\mathrm{1}+\mathrm{4x}^{−\mathrm{2}} \:\Rightarrow\mathrm{du}=−\mathrm{8x}^{−\mathrm{3}} \:\mathrm{dx}\:\mathrm{or}\:\mathrm{x}^{−\mathrm{3}} \:\mathrm{dx}\:=\:−\frac{\mathrm{du}}{\mathrm{8}} \\ $$$$\mathrm{and}\:\frac{\mathrm{4}}{\mathrm{x}^{\mathrm{2}} }\:=\:\mathrm{u}−\mathrm{1}\:\Rightarrow\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\:=\:\frac{\mathrm{u}−\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{then}\:\mathrm{we}\:\mathrm{has}\:\mathrm{I}\:=\:\int\:\frac{\mathrm{1}}{\mathrm{u}}.\frac{\mathrm{u}−\mathrm{1}}{\mathrm{4}}.\left(−\frac{\mathrm{du}}{\mathrm{8}}\right) \\ $$$$\mathrm{I}=−\frac{\mathrm{1}}{\mathrm{32}}\int\:\frac{\mathrm{u}−\mathrm{1}}{\mathrm{u}}\:\mathrm{du}\:=−\frac{\mathrm{1}}{\mathrm{32}}\left(\mathrm{u}−\mathrm{ln}\:\mid\mathrm{u}\mid\right)+\mathrm{c} \\ $$$$\mathrm{I}=−\frac{\mathrm{1}}{\mathrm{32}}\left(\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{4}}{\mathrm{x}^{\mathrm{2}} }−\mathrm{ln}\:\left(\mathrm{x}^{\mathrm{2}} +\mathrm{4}\right)+\mathrm{2ln}\:\mid\mathrm{x}\mid\:\right)+\:\mathrm{c} \\ $$
Answered by Ar Brandon last updated on 01/Feb/21
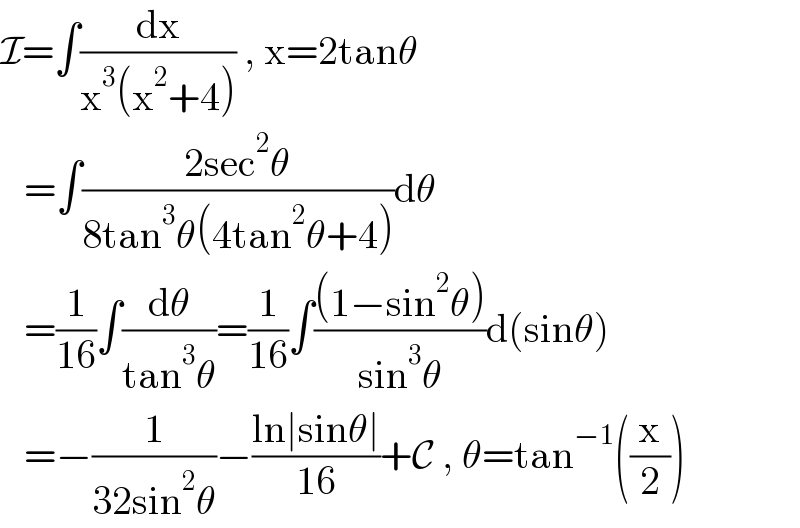
$$\mathcal{I}=\int\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{3}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{4}\right)}\:,\:\mathrm{x}=\mathrm{2tan}\theta \\ $$$$\:\:\:=\int\frac{\mathrm{2sec}^{\mathrm{2}} \theta}{\mathrm{8tan}^{\mathrm{3}} \theta\left(\mathrm{4tan}^{\mathrm{2}} \theta+\mathrm{4}\right)}\mathrm{d}\theta \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{16}}\int\frac{\mathrm{d}\theta}{\mathrm{tan}^{\mathrm{3}} \theta}=\frac{\mathrm{1}}{\mathrm{16}}\int\frac{\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \theta\right)}{\mathrm{sin}^{\mathrm{3}} \theta}\mathrm{d}\left(\mathrm{sin}\theta\right) \\ $$$$\:\:\:=−\frac{\mathrm{1}}{\mathrm{32sin}^{\mathrm{2}} \theta}−\frac{\mathrm{ln}\mid\mathrm{sin}\theta\mid}{\mathrm{16}}+\mathcal{C}\:,\:\theta=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right) \\ $$
