
Question Number 13102 by tawa tawa last updated on 14/May/17
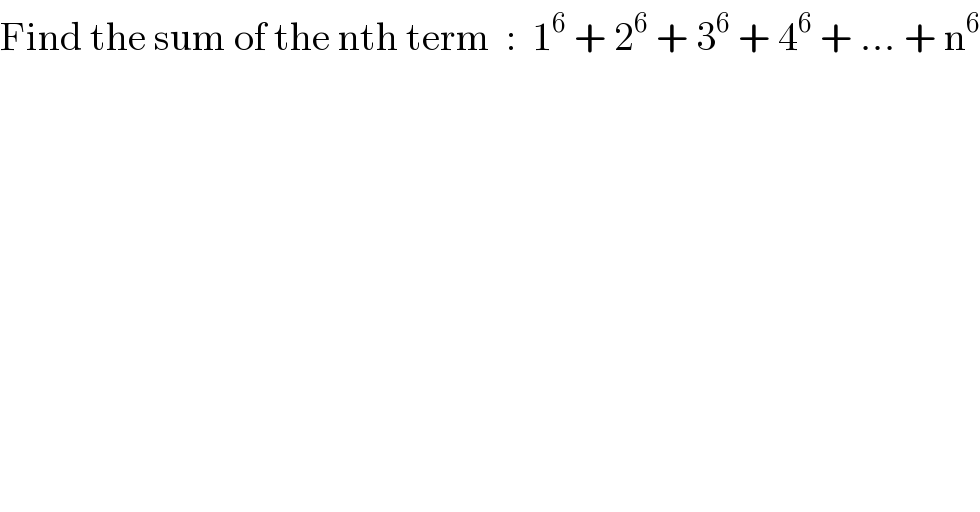
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{nth}\:\mathrm{term}\:\::\:\:\mathrm{1}^{\mathrm{6}} \:+\:\mathrm{2}^{\mathrm{6}} \:+\:\mathrm{3}^{\mathrm{6}} \:+\:\mathrm{4}^{\mathrm{6}} \:+\:...\:+\:\mathrm{n}^{\mathrm{6}} \\ $$
Commented by tawa tawa last updated on 14/May/17
$$\mathrm{please}\:\mathrm{help}\:\mathrm{with}\:\mathrm{this}\:..\: \\ $$
Commented by mrW1 last updated on 14/May/17
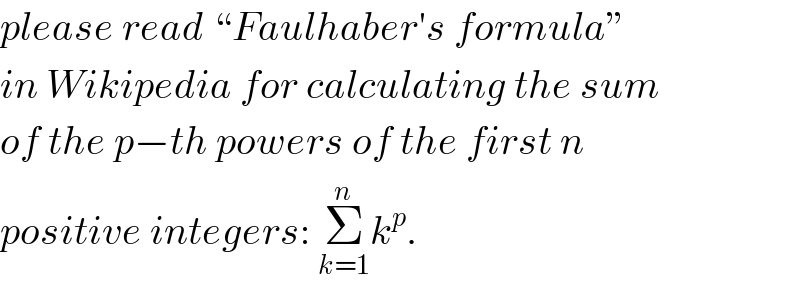
$${please}\:{read}\:``{Faulhaber}'{s}\:{formula}'' \\ $$$${in}\:{Wikipedia}\:{for}\:{calculating}\:{the}\:{sum} \\ $$$${of}\:{the}\:{p}−{th}\:{powers}\:{of}\:{the}\:{first}\:{n} \\ $$$${positive}\:{integers}:\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{{p}} . \\ $$
Commented by mrW1 last updated on 14/May/17

Commented by tawa tawa last updated on 14/May/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}.\: \\ $$
