
Question Number 130925 by Chhing last updated on 30/Jan/21
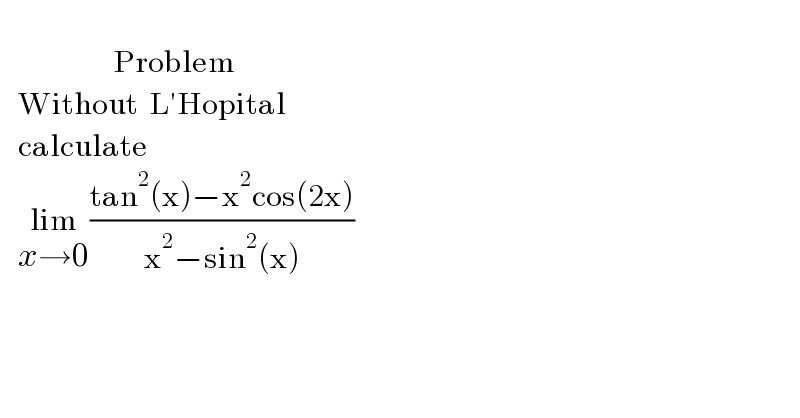
$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{Problem} \\ $$$$\:\:\:\mathrm{Without}\:\:\mathrm{L}'\mathrm{Hopital} \\ $$$$\:\:\:\mathrm{calculate} \\ $$$$\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{tan}^{\mathrm{2}} \left(\mathrm{x}\right)−\mathrm{x}^{\mathrm{2}} \mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{x}^{\mathrm{2}} −\mathrm{sin}^{\mathrm{2}} \left(\mathrm{x}\right)} \\ $$
Commented by malwan last updated on 30/Jan/21
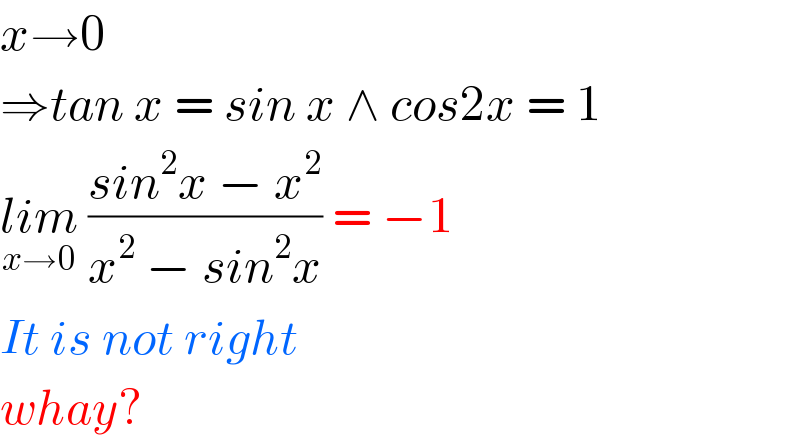
$${x}\rightarrow\mathrm{0} \\ $$$$\Rightarrow{tan}\:{x}\:=\:{sin}\:{x}\:\wedge\:{cos}\mathrm{2}{x}\:=\:\mathrm{1} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\:\frac{{sin}^{\mathrm{2}} {x}\:−\:{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} \:−\:{sin}^{\mathrm{2}} {x}}\:=\:−\mathrm{1} \\ $$$${It}\:{is}\:{not}\:{right} \\ $$$${whay}? \\ $$
Commented by Chhing last updated on 30/Jan/21

$$\:\mathrm{but}\:\:\mathrm{tan}\left(\mathrm{0}\right)=\mathrm{0}\: \\ $$
Commented by malwan last updated on 30/Jan/21

$${and}\:{sin}\left(\mathrm{0}\right)=\mathrm{0} \\ $$
Commented by Chhing last updated on 31/Jan/21

$$\mathrm{Yes},\:\mathrm{sir} \\ $$
Answered by bramlexs22 last updated on 30/Jan/21
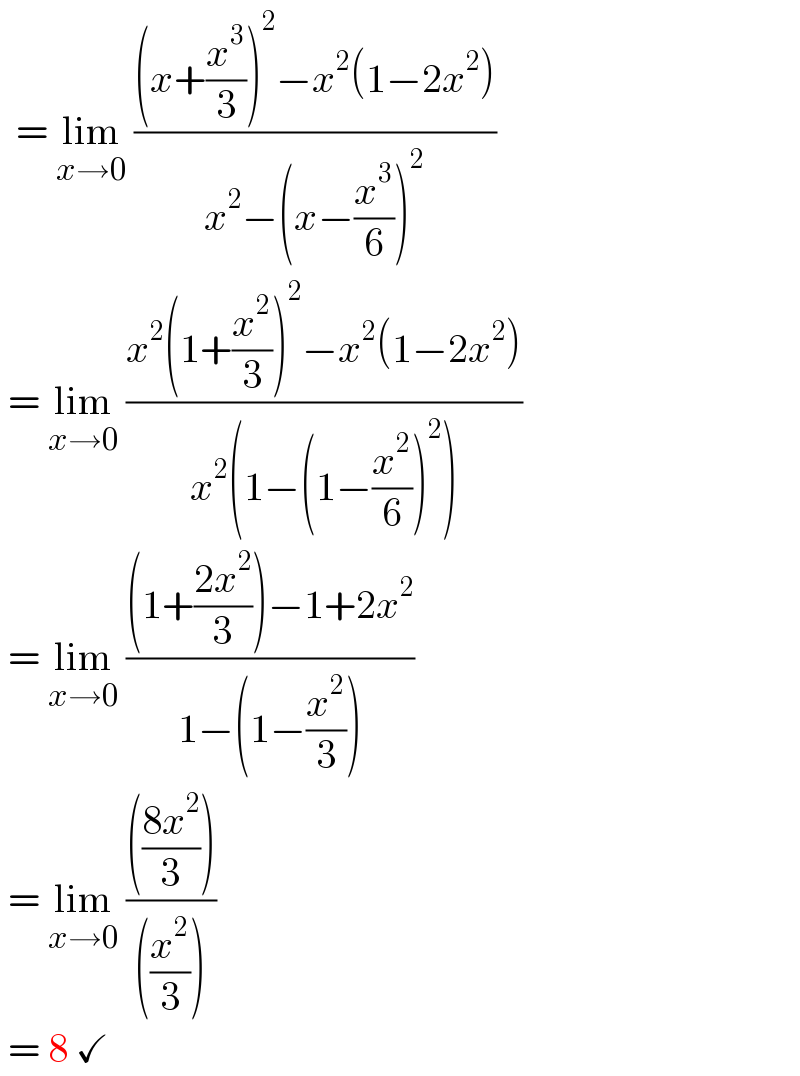
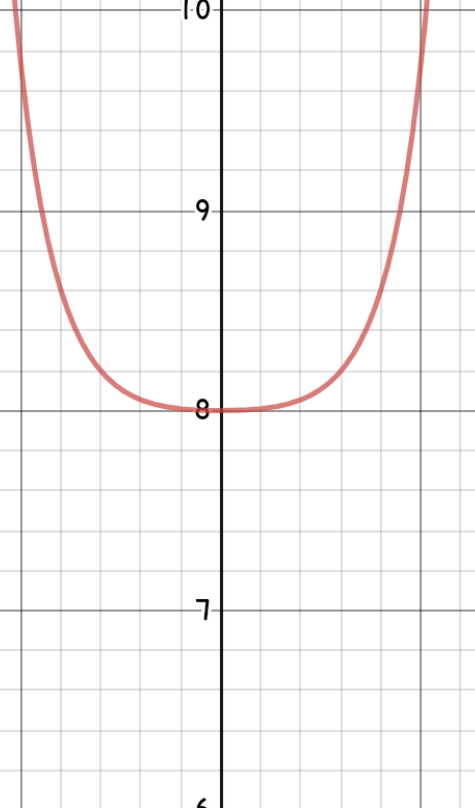
$$\:\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left({x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\right)^{\mathrm{2}} −{x}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{2}{x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} −\left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\right)^{\mathrm{2}} } \\ $$$$\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2}} \left(\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{3}}\right)^{\mathrm{2}} −{x}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{2}{x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} \left(\mathrm{1}−\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}\right)^{\mathrm{2}} \right)} \\ $$$$\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{1}+\frac{\mathrm{2}{x}^{\mathrm{2}} }{\mathrm{3}}\right)−\mathrm{1}+\mathrm{2}{x}^{\mathrm{2}} }{\mathrm{1}−\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{3}}\right)} \\ $$$$\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\frac{\mathrm{8}{x}^{\mathrm{2}} }{\mathrm{3}}\right)}{\left(\frac{{x}^{\mathrm{2}} }{\mathrm{3}}\right)} \\ $$$$\:=\:\mathrm{8}\:\checkmark \\ $$
Commented by bramlexs22 last updated on 30/Jan/21
Answered by benjo_mathlover last updated on 30/Jan/21

$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}−\mathrm{x}^{\mathrm{2}} \left(\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\right)}{\mathrm{x}^{\mathrm{2}} −\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}} \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}−\mathrm{x}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \mathrm{x}+\mathrm{x}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \mathrm{x}}{\left(\mathrm{x}+\mathrm{sin}\:\mathrm{x}\right)\left(\mathrm{x}−\mathrm{sin}\:\mathrm{x}\right)} \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{tan}\:\mathrm{x}+\mathrm{xcos}\:\mathrm{x}\right)\left(\mathrm{tan}\:\mathrm{x}−\mathrm{xcos}\:\mathrm{x}\right)+\mathrm{x}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \mathrm{x}}{\left(\mathrm{x}+\mathrm{sin}\:\mathrm{x}\right)\left(\mathrm{x}−\mathrm{sin}\:\mathrm{x}\right)} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\frac{\mathrm{tan}\:\mathrm{x}}{\mathrm{x}}+\mathrm{cos}\:\mathrm{x}\right)\left(\mathrm{x}+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}−\mathrm{x}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} \right)\right)+\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}\right)}{\left(\mathrm{1}+\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{x}}\right)\left(\mathrm{x}−\mathrm{x}+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}\right)} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}\left(\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{2}}\right)+\mathrm{x}^{\mathrm{3}} −\frac{\mathrm{x}^{\mathrm{5}} }{\mathrm{6}}}{\mathrm{2}\left(\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}\right)}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{8}}{\mathrm{3}}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{6}}}{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$\:=\:\mathrm{8}.\: \\ $$
Commented by bramlexs22 last updated on 30/Jan/21

$${yeahhh}...\checkmark \\ $$
Commented by Chhing last updated on 30/Jan/21

$$\mathrm{Thank}\:\mathrm{you} \\ $$
Commented by Chhing last updated on 30/Jan/21

$$\mathrm{Thank}\:\mathrm{you} \\ $$
